Altissima: Pembahasan Tugas harian 1: garis singgung lingkaran kelas 8 SMP (27 Januari 2022)

Latihan Soal Garis Singgung Lingkaran
Kelas 8 SMP
Tugas dikumpulkan pada 27 Januari 2022
dikirim langsung melalui alamat email: altissimastudycenter@gmail.com

Kerjakan soal berikut dengan benar

Dari garis-garis k, l, m, n, dan p pada gambar di atas, manakah yang merupakan garis singgung lingkaran?

jawab:

Salah satu ciri khas garis singgung lingkaran adalah tidak memotong lingkaran di dua titik tetapi menyentuh lingkaran di satu titik. Oleh karena itu garis yang menyinggung lingkaran pada gambar tersebut adalah garis l, garis n dan garis j.
Lukislah pada kertas berpetak lingkaran berpusat di titik O(0, 0) dengan jari-jari 5 satuan panjang. Selanjutnya lukislah garis singgung lingkaran yang melalui titik A(0, 5).

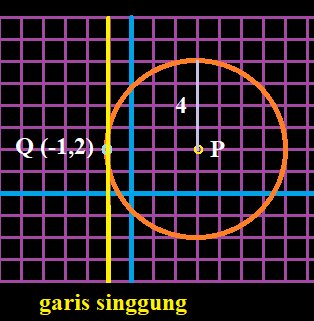
jawab
Lukislah pada kertas berpetak lingkaran dengan pusat di titik P(3, 2) dan jari-jari 4 satuan panjang. Selanjutnya, lukislah garis singgung lingkaran yang melalui titik Q(–1, 2).

jawab :
Berdasarkan keterangan pada gambar berikut, hitunglah panjang setiap garis singgung lingkarannya.

jawab

(i) $AB=\sqrt{OB^2-OA^2}=\sqrt{7^2-5^2}=\sqrt{49-25}=\sqrt{24}=2\sqrt 6$ cm

(ii) $PQ=\sqrt{OP^2-OQ^2}=\sqrt{20^2-12^2}=\sqrt{400-144}=\sqrt{256}=16$ cm

(iii) $XY=\sqrt{OX^2-OY^2}=\sqrt{26^2-10^2}=\sqrt{676-100}=\sqrt{576}=24$ cm
Perhatikan gambar berikut:

Garis AB dan BC adalah garis singgung lingkaran yang melalui titik A. Jika OA = 10 cm dan OB = 26 cm maka tentukan
a. panjang garis singgung AB;
b. luas layang-layang OBAC;
c. panjang tali busur AC.
jawab

a. $AB=\sqrt{OB^2-OA^2}=\sqrt{26^2-10^2}=\sqrt{676-100}=\sqrt{576}=24$ cm

b. Luas $\displaystyle \bigtriangleup OAB=\frac{1}{2} \times AB \times OA= \frac{1}{2}\times 24 \times 10 = 120$ cm$^2$

Jadi luas layang-layang $= 2\times \bigtriangleup OAB = 2 \times 120=240$ cm$^2$

c. Misalkan D adalah titik potong diagonal layang-layang
Dengan menggunakan perbandingan luas kita dapatkan

Luas $\displaystyle \bigtriangleup OAB=\frac{1}{2} \times OB \times AD$

$\displaystyle 120 =\frac{1}{2} \times 26 \times AD$

$\displaystyle AD =\frac{120}{13} $

dengan demikian panjang tali busur layang $\displaystyle AC = 2 \times AD = 2 \times \frac {120}{13} = \frac {240}{13}$ cm
Perhatikan gambar berikut.

Berdasarkan gambar tersebut, benar atau salahkah pernyataan-pernyataan berikut?
a. AB sejajar PQ
b. AP tegak lurus PQ
c. AB = CD
d. AB = PQ
e. AP tegak lurus AB di titik A

jawab:
a. salah karena $\angle PAB \neq \angle APQ$ dan $\angle ABQ \neq \angle PQB$
b. Benar berdasarkan sifat garis singgung lingkaran.
c. Benar berdasarkan sifat garis singgung persekutuan luar lingkaran
d. Salah karena AB adalah ruas garis singgung persekutuan luar lingkaran, sedangkan PQ jarak titik pusat kedua lingkaran. berdasarkan sifat garis singgung persekutuan luar panjang PQ > panjang AB
Panjang jari-jari dua lingkaran masing-masing adalah 12 cm dan 5 cm. Jarak kedua titik pusatnya adalah 24 cm. Hitunglah
a. panjang garis singgung persekutuan dalam;
b. panjang garis singgung persekutuan luarnya.

Jawab
diketahui p = 24, R = 12 dan r = 5
a. $d = \sqrt{p^2-(R+r)^2}=\sqrt{24^2-(12+5)^2}=\sqrt{576 - 289}=\sqrt {287}$ cm

b. $d =\sqrt{p^2-(R-r)^2}=\sqrt{24^2-(12-5)^2}=\sqrt{576 - 49}=\sqrt {527}$ cm
Perhatikan gambar di atas.

Panjang jari-jari lingkaran yang berpusat di O adalah 9 cm dan panjang jari-jari lingkaran yang berpusat di P adalah 4 cm. Jika panjang garis singgung persekutuan luarnya 12 cm, tentukan
a. jarak kedua pusat lingkaran;
b. luas segi empat yang diarsir

Jawab

Diketahui d = 12 cm, R = 9 cm dan r = 4 cm

a. $p = \sqrt {d^2+(R-r)^2}=\sqrt{12^2+(9-4)^2}=\sqrt{144 + 25}=\sqrt {13}$ cm
b. Luas daerah yang diarsir $=2 \times \begin {matrix} luas & trapesium \end {matrix}= 2\times \frac{1}{2}\times (R+r) \times AB=2 \times \frac{1}{2} \times (9+4)\times 12 =156$ cm$^2$
Panjang garis singgung persekutuan dalam dua lingkaran adalah 24 cm dan jarak kedua pusatnya adalah 26 cm. Jika panjang salah satu jari-jari lingkaran 6 cm, hitunglah panjang jari-jari lingkaran yang lain.

Jawab
diketahui d = 24 cm, p =26 cm dan R = 6 cm
$R + r = \sqrt{p^2 - d^2}$
$ 6 + t = \sqrt{26^2-6^2}=\sqrt{676-576}=\sqrt{100}=10$ $\Leftrightarrow$ $r =10-6=4 cm$
Panjang jari-jari dua buah lingkaran yang berpusat di O dan P masing-masing adalah 8 cm dan 4 cm. Jarak kedua titik pusatnya 20 cm.
a. Lukislah garis singgung persekutuan dalamnya.
b. Hitunglah panjang garis singgung persekutuan dalam tersebut.