Bangun ruang

 A. Konsep dasar bangun ruang

        Dalam kehidupan sehari-hari, kita dapa menemukan berbagai macam bentuk bangun ruang  yang ada disekitar kita. Misalnya kotak susu, kaleng biskuit, lemari bola, piramida, dadu, dll. Semua bangun ruang yang disebut tadi memiliki tiga unsur dasar yang terdiri dari rusuk, sisi, dan titik sudut. Karena itulah maka bangun ruang dapat dinamakan bangun tiga dimensi. Karena struktur dasarnya tersusun dari tiga unsur tersebut, maka setiap bangun ruang memiliki volume.
        Secara keseluruhan, bangun ruang dapat dibagi ke dalam dua macam, yakni bangun ruang sisi datar dan bangun ruang sisi lengkung. Bangun ruang sisi datar adalah bangung ruang yang permukaan sisinya berbentuk datar. Misalnya kotak susu, piramida mesir, coklat tobleron, rubik, dadu, dll. Sementara bangun ruang sisi lengkung memiliki sisi yang tidak datar dan cendrung melengkung. Misalnya bola, tong minyak, kaleng susu, topi pak tani, dll.

contoh bangun ruang sisi datar

Contoh bangun ruang sisi lengkung

B. Macam-macam bangun ruang
Berdasarkan bentuk permukaannya, bangun ruang dapat digolongkan dalam beberapa kelompok berikut:

1. Prisma
   Bangun ruang prisma memiliki beberapa unsur berikut ini
        a. Bagian alas dan atapnya berbentuk persegi banyak, sejajar dan kongruen
        b. Bagian permukaan sisi tegaknya (selimut) biasanya berbentuk persegi/persegi panjang atau 
            jajaran genjang.
        c. Bagian permukaan sisinya (selimut) umumnya tegak lurus terhadap bidang alasnya. Namun
            ada juga prisma yang miring terhadap bidang alasnya.
        d. Bagian rusuk tegaknya umumnya juga tegak lurus terhadap bidang alasnya.
        e. Memiliki jumlah sudut sebanyak 2 kali jumlah segi pada bidang alasnya
        f. Memiliki jumlah rusuk sebanyak 3 kali jumlah segi pada bidang alasnya.
        g. Istilah terhadap jenis bangun prisma umumnya sangat terkait dengan bentuk alasnya
            misalnya prisma segitiga berarti alasnya berbentuk segitiga.
                           prisma segi delapan berarti alasnya berbentuk segi delapan 
   
   Rumus umum yang berlaku pada bangun ruang berbentuk prisma adalah:
                  
                   Luas Alas = $ 2\times$ Luas Alas + Luas Selimut
                                    $=2 \times$ luas alas + keliling alas $\times$ tinggi
   
                   Volume = Luas Alas $\times $  Tinggi Prisma  
   
                   banyaknya sisi prisma segi$-n \displaystyle = n+2$
   
                   banyaknya diagonal bidang alas prisma segi$-n \displaystyle = \frac{n(n-3)}{2}$
   
                   banyaknya bidang diagonal prisma segi$-n \displaystyle = \frac{n(n-3)}{2}$
   
                   banyaknya diagonal ruang prisma segi$-n \displaystyle = n(n-3)$
   
   
   

   

   contoh bangun prisma

   
   Beberapa jenis bangun ruang yang masuk dalam kelompok prisma diantaranya 
   
   
• Prisma Segitiga
  ciri-ciri :
  

  a. Memiliki alas dan atap segitiga yang sebangun.
  b. Memiliki lima bidang sisi. Sisi prisma segitiga terdiri dari bangun datar persegi panjang dan segitiga.
  c. Memiliki 3 bidang sisi tegak.
  d. Memiliki 9 rusuk. Rusuk bangun ruang adalah pertemuan dari dua sisi yang menyusunnya.
  5. Memiliki 6 titik sudut. Titik sudut adalah titik pertemuan dari beberapa rusuk.

  
  gambar bangun ruang prisma segitiga
  
  

  

  Contoh prisma segitiga dan bagannya

  
  
  
  
  Contoh jaring-jaring prisma segitiga
  
  

  

  Jaring-jaring prisma segitiga

  
  
  
  
• Prisma Segi Empat
  Prisma segi empat merupakan sebuah bangun ruang tiga dimensi yang alas dan penutupnya memiliki bentuk datar segi empat baik berupa persegi panjang, persegi, belah ketupat, layang-layang, jajar genjang dan trapesium, serta selimut sisi samping berbentuk persegi panjang.  
  
  ciri-ciri prisma segi empat:
  a. Bangun ruang memiliki 4 sisi yang berbentuk persegi/persegi panjang
  b. Memiliki 8 titik sudut pada bagun ruangnya
  c. Memiliki 12 rusuk, 4 diantaranya merupakan rusuk tegak.
  d. Memiliki  4 diagonal ruang
  
  Bangun ruang yang termasuk prisma segi empat adalah 
  a. Kubus
      Kubus merupakan prisma segi empat yang seluruh sisinya berbentuk persegi. Semua sisi
      yang berhimpitan saling tegak lurus. Beberapa contoh kubus adalah dadu dan rubik.
     
      ciri-ciri yang lainnya:
          a. Memiliki 12 rusuk sama panjang
          b. memiliki 6 sisi berbentuk persegi dan seluruh sudutnya membentuk 90$^o$
          c. Memiliki 12 diagonal sisi, 6 bidang diagonal, 4 diagonal ruang. 
          d. Memiliki 8 titik sudut
          e. Memiliki 12 diagonal bidang yang sama panjang
          
        Rumus yang berlaku untuk kubus adalah :
  
               Luas permukaan = $6\times a^2$  dimana a adalah panjang sisi persegi
  
               Volume    =    $ a^3$
  
  
  

  

  contoh kubus beserta jaring-jaringnya

  
  

  

  Kubus dan bagannya

  
  
  
  
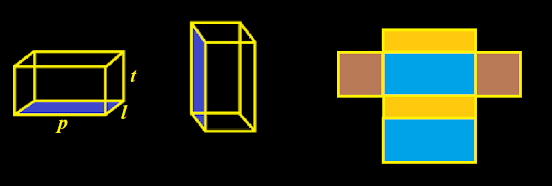
  b. Balok
      Bentuk balok menyerupai kubus, namun alas dan atapnya berbentuk persegi panjang
      4 sisi-sisi selimutnya berbentuk persegi panjang dan 2 sisi lain yang berhadapan bisa
      berbentuk persegi/persegi panjang. Contoh balok adalah kardus, kotak susu, brankas
      besi, dll
  
      Beberapa ciri lainnya adalah :
           a. Memiliki 12 rusuk, 4 rusuk yang saling sejajar berukuran sama panjang
           b. Memiliki 8 titik sudut
           c. Memiliki 6 sisi yang saling tegak lurus  satu dengan sisi yang berhimpitan
           d. Memiliki 12 diagonal sisi, 6 diagonal bidang dan 4 diagonal ruang.
           e. Memiliki 6 bidang diagonal yang berbentuk persegi panjang dan tiap pasangnya
               kongruen
  
     Rumus yang berlaku pada balok adalah
  
              Luas permukaan = $ 2\times (p\times l+p\times t+l\times t)$
  
             Volume $=p\times l \times t$
  
     dimana p = panjang, l = lebar dan t = tinggi
   
     gambar balok
  
     

  

  contoh balok beserta jaring-jaringnya

  
  
  
  
  
• Tabung
  
  
  Tabung adalah suatu bangun ruang yang dibatasi oleh sisi alas dan sisi atas berbentuk lingkaran. Sedangkan bidang sisi tegak pada tabung membentuk lengkungan yang sering disebut dengan selimut tabung. Jarak antara sisi alas dengan sisi tutup merupakan tinggi sebuah tabung. Contoh benda berbentuk bangun ruang tabung yaitu kaleng susu, kaleng minuman dan drum.
  
  Ciri-ciri tabung adalah sebagai berikut:
     a. Memiliki 3 buah sisi (dua buah lingkaran dan 1 selimut berbentuk persegi panjang)
     b. Memiliki 2 buah rusuk lengkung
     c. Memiliki alas dan atap/tutup berbentuk lingkaran
     d. Tidak memiliki sudut
  
  
  Rumus umum tabung :
         
         Luas permukaan  $\displaystyle = 2 \times$ lingkaran + luas selimut
                                      $\displaystyle = 2 \times$ lingkaran + keliling alas $\times \pi \times t_{tabung}$
                                      $\displaystyle = 2 \times \pi \times r^2 +  \pi \times D \times t_{tabung}$
                                      $\displaystyle = 2 \times \pi \times r^2 + 2 \times \pi \times r \times t_{tabung}$
                                      $\displaystyle = 2 \times \pi \times r (r +  t_{tabung}) $
         
         Volume  = $\pi \times r^2 \times t$
  
  dimana  r = jari-jari alas lingkaran,          D = diameter alas lingkaran
  
                $t_{tabung}$ = tinggi tabung                $\displaystyle \pi = \frac {22}{7}=\approx 3,14$                           
  
  
  

  

  Contoh tabung beserta jaring-jaringnya

  
  
  
  
2. Limas
   
   Limas adalah jenis bangun ruang yang tersusun atas sebuah alas berbentuk segi-n dengan setiap sisi tegak saling bertemu di satu titik. Alas limas dapat berbentuk segitiga, segiempat, lingkaran dll. Limas yang memiliki alas berbentuk segiempat biasanya disebut piramida dan limas yang alasnya berbentuk lingkaran biasanya disebut kerucut
   
   Rumus yang berlaku pada limas adalah
   
               Luas permukaan = jumlah semua luas sisi permukaannya
   
               Volume $\displaystyle =\frac{1}{3} \times$ luas alas limas $\times$  tinggi limas
   
               Banyaknya sisi limas segi$-n \displaystyle = n+1$
   
               Besar sudut limas segi-n beraturan $\displaystyle = \frac{(n-1)\times 180^o}{n}$
   
               Besar 1 sudut pusat segi-n berarturan $\displaystyle = \frac{360^o}{n}$
   
   

• Limas Segitiga
  ciri-ciri limas segitiga:
       a.  memiliki alas berbentuk segitiga,
       b.  tidak memiliki diagonal ruang maupun sisi,
       c. Memiliki 4 sudut, 4 sisi dan 6 rusuk
  
  

  

  Contoh Limas segitiga beserta jaring-jaringnya

  
  
  
• Limas Segi Empat 
  ciri-ciri limas segiempat:
       a.  memiliki alas berbentuk segiempat,
       b.  memiliki 2 diagonal ruang dan 2 diagonal sisi,
       c.  Memiliki 5 sudut, 5 sisi dan 8 rusuk
  
  

  

  Contoh limas segiempat beserta jaring-jaringnya

  
  
  
  
• Kerucut
  
  
  Ciri dari bangun ruang ini adalah
       a. hanya memiliki 2 sisi berbentuk lingkaran dan juring lingkaran
       b. memiliki  1 titik sudut, dan  mempunyai 1 rusuk berbentuk melengkung, 
  
  
  Rumus yang berlaku pada kerucut:
  
            Luas Permukaan $=\pi \times r \times S + \pi \times r^2$ 
  
            Volume $\displaystyle =\frac{1}{3} \pi \times r^2 \times t$
  
  dimana r = jari-jari, t = tinggi kerucut dan S = garis pelukis 
  

  
  

  

  gambar kerucut

  
  
  

  
  

      3. Bola

Ciri-ciri bola:
     a. Hanya memiliki 1 buah sisi berbentuk bidang lengkung
     b. Setiap permukaan sisinya memiliki jarak yang sama terhadap 1 titik pusat

     c. Tidak memiliki sudut
     d. tidak memiliki rusuk

     e. Memiliki jari-jari yang tak berhingga banyaknya
     

        Rumus yang berlaku pada bola

                 Luas permukaan $= 4 \times \pi \times r^2$ 

                 Volume $\displaystyle \frac{4}{3} \times \pi \times r^3$
    

        Dimana  r = jari-jari bola   dan   $\displaystyle \pi = \frac {22}{7} \approx 3,14$

Contoh bangun ruang bola

== Selamat Belajar ==

NB: Sebagai latihan soal, kalian bisa mengerjakan tugas harian di tautan berjudul "Latihan soal volume bangun ruang."