Menentukan panjang sabuk lingkaran

Kalian tentu tahu rantai sepeda bukan? ya... rantai sepeda merupakan bagian dari sepeda yang digunakan sebagai penggerak sepeda. Nah, apakah kalian dapat menghitung panjang rantai sepeda jika diketahui panjang jari-jari gear sepeda? Pada pembahasan kali ini kita akan diperkenalkan contoh penyelesaian bagaimana menghitung panjang sabuk lingkaran. Dengan kalian mengetahui bagaimana langkah-langkah perhitungannya, kalian akan dapat menentukan sendiri panjang rantai sepeda.

Contoh 1

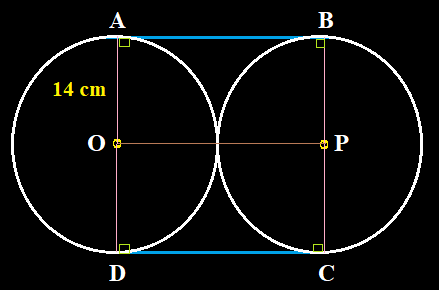
Dua buah gear sepeda memiliki jari-jari sama sebesar 14 cm. Tentukan panjang rantai yang menghubungkan gear speda tersebut!

jawab  
perhatikan gambar berikut

Pada gambar di atas kita mengetahui bahwa dua gear memiliki jari-jari yang sama yakni 14 cm. Dengan demikian panjang $AB = CD = 2\times 14 = 28$ cm. Busur $\overset {\frown}{AD}=\overset {\frown}{BC}$. Kita akan menentukan panjang busur tersebut untuk mengetahui panjang rantai yang mengelilingi gear 1 dan gear 2.

Perhatikan bahwa busur $\overset AD$ merupakan $\frac{1}{2}$ keliling lingkaran. Karena busur Busur $\overset {\frown}{AD}=\overset {\frown}{BC}$ , Maka jelas bahwa jumlah panjang rantai yang mengelilingi gear 1 dan gear 2 tidak lain adalah keliling 1 buah gear itu sendiri. Sehingga kita dapatkan

panjang sabuk = keliling lingkaran  $+ AB + CD \displaystyle = \pi \times diameter + 28 + 28 = \frac {22}{7} \times 28 + 56 = 88 + 56 = 144$ cm

Jadi panjang rantai yang dibutuhkan adalah 144 cm  

Contoh 2

Diketahui 3 buah lingkaran memiliki jari-jari 7 cm diikat sedemikian rupa seperti gambar berikut ini:

Hitunglah panjang tali yang dibutuhkan untuk mengikat ke tiga lingkaran tersebut!

Jawab:
perhatikan gambar berikut ini

Ketiga lingkaran masing-masing memiliki titik pusat di A, B dan C. Karena masing-masing lingkaran memiliki jari-jari 7 cm, maka  panjang AB = BC = AC = 7 +7 =14 cm. $\bigtriangleup ABC$ merupakan segitiga sama sisi, sehingga $\angle ABC = \angle BCA = \angle BAC = 60^o$. Selain itu karena letaknya yang kosentris terhadap segitiga sama sisi ABC, maka panjang busur $\overset{\frown}{DI}=\overset{\frown}{UF}=\overset{\frown}{GH}$, Kita akan menentukan panjang masing busur ini untuk menentukan panjang tali yang melingkari masing-masing lingkaran.

Perhatikan lingkaran yang berpusat di A
karena ABDE, BCGF dan  ACHI adalah persegi panjang maka $\angle DAB = \angle IAC=90^2$ dan  = AB = 14
Dengan demikian kita dapat menentukan besar sudut $\angle DAI$ yakni
$\angle DAI =360^o - \angle DAB - \angle IAC - \angle BAC=360^o-90^o-90^o-60^o=120^o$ 

Berdasarkan teori garis singgung lingkaran, maka kita dapatkan

Panjang busur $\displaystyle \overset{\frown}{DI}= \frac{\angle DAI}{360^o}\times \begin {matrix} keliling&lingkaran&A \end {matrix}=\frac {120^o}{360^o}\times \frac {22}{7}\times 14=\frac {1}{3}\times 44=\frac {44}{3}$ cm

Dengan demikian panjang sabuk ketiga lingkaran tersebut dapat kita cari, yakni

Panjang sabuk  $=\overset{\frown}{DI}+\overset{\frown}{UF}+\overset{\frown}{GH}+ DE + FG + HI$
        $\Leftrightarrow$           $\displaystyle = 3 \times (\overset{\frown}{DI} + AB) = 3 \times (\frac {44}{3}+14)=44 +42=86$ cm

Jadi panjang tali yang dibutuhkan $\geq$ dari 86 cm.

Contoh 3

Gambar di atas adalah penampang enam buah drum yang berbentuk tabung dengan jari-jari 24 cm. Hitunglah panjang tali minimal yang diperlukan untuk mengikat enam buah drum tersebut.

Jawab:
sama seperti pada contoh 2, keenam lingkaran tersebut tersusun secara konsentris terhadap segitiga sama sisi yang panjang sisinya $= 4 \times 24 = 96$ cm. Karena kedudukannya yang konsentris maka besar sudut yang terbentuk pada busur yang dikeliling tali (lingkaran 1, 4 dan 6) sebesar $120^o$. Dengan demikian

panjang busur $=3 \times$ panjang sisi segitiga sama sisi + $3 \times$ panjang busur yang dikeliling tali $ =3 \times 96 + 3 \times \frac {120^o}{360^o}\times 3,14 \times 48 =288 +150,72= 438,72$ cm

==== Selamat Belajar ====