Pembahasan Soal Matematika Kelas 7 SMP materi Kubus dan Balok

Tugas Harian
Kubus dan Balok

==============000==============

Kerjakan soal-soal berikut di buku tugasmu.

1. Perhatikan gambar berikut!
   
   

   

   
   
   Manakah pernyataan-pernyataan berikut yang benar?
            a. Rusuk IJ // LK // MN // PO .
            b. Rusuk JN // KO // IM // LP .
            c. Rusuk MN tidak sejajar dengan LP .
            d. Rusuk IL // JK // NO // MP
   
   Jawab:
   Semua pernyataan tersebut benar
   
   
2. Lukislah sebuah kubus KLMN.OPQR pada kertas berpetak dengan panjang rusuk 5 satuan.
       a. Sebutkan pasangan ruas garis yang sejajar.
       b. Sebutkan pula tiga pasang ruas garis yang bersilangan.
   
   jawab
   
   

   

   
   a. Pasangan garis yang sejajar
          a.1 garis KL // MN // QR //OP
          a.2 garis KO // LP // MQ //NR
          a.3 garis KN // LM // PQ //OR
   
   b, Pasangan garis yang bersilangan
         b.1 KO dengan MN dan QR
         b.2 KL dengan MQ dan NR
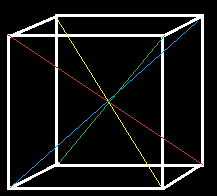
         b.3 KN dengan LM dan MQ
   
   
   
3. Lukislah sebuah balok ABCD.EFGH pada kertas berpetak dengan ukuran panjang 5 satuan, lebar 3 satuan, dan tinggi 3 satuan.
           a. Lukislah semua diagonal bidangnya.
           b. Berapa banyak diagonal bidang yang dapat dilukis?
   
   Jawab
           a
   
   

   

   
   
             b. Ada 12 diagonal sisi
   
   
   
4. Pada bangun balok yang telah kalian lukis (soal nomor 3), lukis diagonal ruangnya. Ada berapa banyak diagonal ruang yang dapat dilukis?
   
   

   

   
   
   
5. a. Lukislah sebuah kubus EFGH.IJKL pada kertas berpetak dengan panjang rusuk 6 satuan dan
       EFGH sebagai bidang alasnya.
   b. Hitunglah jumlah panjang diagonal bidang pada kubus tersebut.
   c. Hitung pula jumlah panjang diagonal ruang pada kubus tersebut.
   
   Jawab
   a. 

   

   
   b. 

   
   
   

        Ada 12 diagonal bidang pada kubus
   c. 

   

   
       Ada 4 diagonal ruang pada kubus
   
   
6. Lukislah sebuah kubus dan sebuah balok. Dapatkah kalian menentukan sifat-sifat kubus dan balok tersebut dipandang dari sisi, rusuk, dan titik sudutnya?
   
   Jawab
   

   

   
   Ciri-ciri Kubus
           a. Memiliki 12 rusuk sama panjang
           b. memiliki 6 sisi berbentuk persegi dan seluruh sudutnya membentuk 90$^o$
           c. Memiliki 12 diagonal sisi, 6 bidang diagonal, 4 diagonal ruang. 
           d. Memiliki 8 titik sudut
           e. Memiliki 12 diagonal bidang yang sama panjang
           f. Setiap sisi yang berhimpitan saling tegak lurus satu dengan yang lainnya.
   
   Ciri-ciri balok
            a. Memiliki 12 rusuk, 4 rusuk yang saling sejajar berukuran sama panjang
            b. Memiliki 8 titik sudut
            c. Memiliki 6 sisi yang saling tegak lurus  satu dengan sisi yang berhimpitan
            d. Memiliki 12 diagonal sisi, 6 diagonal bidang dan 4 diagonal ruang.
            e. Memiliki 6 bidang diagonal yang berbentuk persegi panjang dan tiap pasangnya
                kongruen
            f. Setiap sisi yang berhimpitan saling tegak lurus terhadap yang lainnya
   
   
7. Lukislah kubus KLMN.OPQR.
      a. Berbentuk apakah bangun KLMN? Berapakah luasnya?
      b. Berbentuk apakah bangun LMQP? Berapakah luasnya?
      c. Menurutmu, bagaimana luas setiap sisi pada suatu kubus?
   
   Jawab
   

   

   
       a. Bangun KLMN berbentuk persegi
       b. Bangun LMQP berbentuk persegi
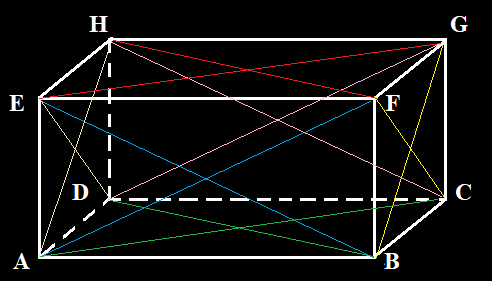
       c, Luas setiap sisi pada kubus adalah luas persegi yakni $sisi \times sisi$
   
   
   
8. Lukislah balok ABCD.EFGH.
      a. Berbentuk apakah bangun ABCD, BCGF, dan ABFE? Tentukan luasnya.
      b. Tentukan pula luas sisi-sisi balok yang lain.
      c. Apa yang dapat kalian simpulkan dari jawaban a dan b?
   
   Jawab
   

   

   
        a. Bangun ABCD berbentuk persegi panjang dengan luas $=AB \times BC$
            Bangun BCGF berbentuk persegi panjang dengan luas $=CG \times BC$
            Bangun ABFE berbentuk persegi panjang dengan luas $=AB \times BF$
   
        b. Bangun EFGH berbentuk persegi panjang dengan luas $=EF \times FG$
            Bangun CDHG berbentuk persegi panjang dengan luas $=CD \times DH$
            Bangun ADHE berbentuk persegi panjang dengan luas $=AD \times DH$
   
         c. Jika $AB = p, BC = l$ dan $AE = t$, maka luas permukaan balok dapat dicari yakni 
             Luas permukaan balok $ = 2 \times \left ( p\times l + p \times t + l \times t \right )$
    
9. Lukislah sebuah kubus dengan panjang rusuk 4 cm. Berapakah jumlah panjang rusuk kubus tersebut?
   
   

   

   
   Jumlah semua rusuk kubus adalah 12 buah. Karena masing-masing rusuk panjangnya 4 cm, maka total jumlah panjang seluruh rusuk $= 12 \times 4 = 48 $ cm 
   
   
10. Sediakan sebuah kaleng bekas roti atau susu. Amatilah kaleng tersebut. Bagaimana sisi kaleng tersebut? Berapakah banyaknya rusuk kaleng tersebut?
    
    Jawab
    Sisi kaleng berbentuk persegi panjang. Banyaknya rusuk pada kaleng yang berbentuk balok/kubus adalah 12 buah.
    
    
    
11. Sukma memiliki kawat sepanjang 156 cm. Ia ingin menggunakan kawat tersebut untuk membuat kerangka kubus. Berapa panjang rusuk kubus agar kawat tidak bersisa?
    
    Jawab
    Banyaknya rusuk yang dibutuhkan adalah 12 buah. Dengan demikian panjang setiap rusuk dapat dihitung yakni
    
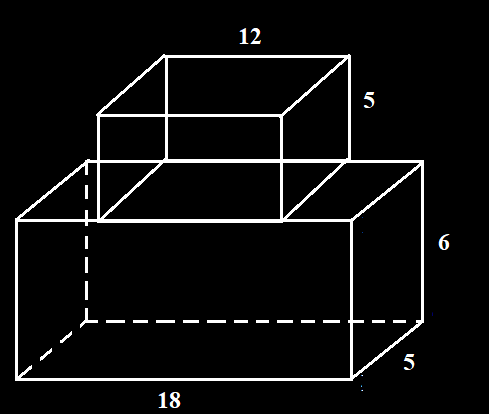
             $\displaystyle r =\frac{156}{12}=13$ cm
    
    
    
12. Diketahui sebatang kawat mempunyai panjang 236 cm. Kawat itu akan dibuat model kerangka berbentuk kubus dan balok. Jika ukuran balok tersebut $(12 \times 8 \times 5)$ cm, tentukan panjang rusuk kubus.
    
    Jawab
    
    Panjang total kawat untuk balok $ = 4 \times ( p + l + t) =4 \times (12 + 8 + 5)=4 \times 25=100$ cm
    
    Sisa kawat yang akan digunakan = 236 - panjang total kawat balok = 256 - 100 = 156 cm
    
    Panjang setiap rusuk kubus yang akan dibuat $\displaystyle =\frac {156}{12}=13$ cm
    
    
    
13. Perhatikan gambar di bawah.
    
    

    

    
    Berapa panjang kawat yang diperlukan untuk membuat model kerangka seperti gambar di atas?
    
    Jawab
    
    Jumlah kawat yang dibutuhkan :
       
             Balok besar $=4 \times (18+5+6) =4\times 29 =  116$
             Balok kecil $= \underline {4 \times (5+5)+2 \times 12 =40 + 24 =64}$ +
                                                 total = 180
    
    
    
14. Hitunglah panjang kawat yang diperlukan untuk membuat kotak kapur tulis berukuran $(6 \times 4 \times 5)$ cm.
    
    Jawab
    panjang kawat yang diperlukan $=4\times (6+4+5)=4\times 15 =60$ cm
    
    
    
15. Made akan membuat 15 buah kerangka balok yang masing-masing berukuran $30 \times 20 \times 15$ cm. Bahan yang akan digunakan terbuat dari kawat yang harganya Rp1.500/m.
        a. Hitunglah jumlah panjang kawat yang diperlukan untuk membuat balok tersebut.
        b. Hitunglah biaya yang diperlukan untuk membeli bahan/kawat.
    
    Jawab
        a. Jumlah kawat yang diperlukan $= 4\times (30+20+15)=4\times 65=260$ m
        b. Biaya yang diperlukan $= 260 \times 1500 = 390.000$
    
    
    
16. Di antara gambar berikut, manakah yang merupakan jaring-jaring kubus?
    
    
    
    
    
    Jawab
    
    Di antara gambar tersebut, hanya gambar a dan gambar d yang bukan jaring-jaring kubus. Sementara yang lainnya merupakan jaring-jaring kubus.
    
    
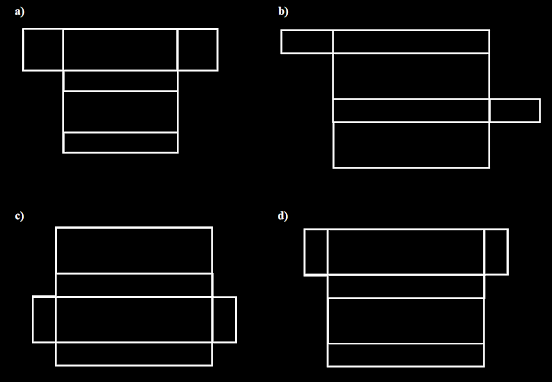
17. Di antara gambar berikut, manakah yang merupakan jaring-jaring balok?
    
    
    
    
    
    Jawab
    hanya gambar a yang bukan jaring-jaring balok
    |
    
    
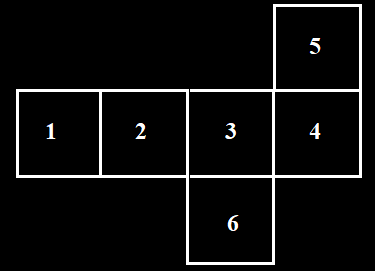
18. Perhatikan jaring-jaring kubus pada gambar di bawah.
    
    
    
    
    
    Jika nomor 3 sebagai alas kubus, nomor berapakah yang menjadi tutup kubus?
    
    Jawab
    Nomor 1
    
    
19. Buatlah model balok dengan panjang 6 cm, lebar 4 cm, dan tinggi 5 cm. Carilah kemungkinan-kemungkinan jaring-jaring balok yang berlainan yang dapat dibuat dari balok tersebut. Ada berapakah jaring-jaring balok yang dapat kalian buat?
    
    Jawab
    
    Beberapa contohnya adalah
    
    
    
    
     
    
20. Hitunglah luas permukaan kubus dengan panjang setiap rusuknya sebagai berikut.
         a. 4 cm
         b. 10 cm
         c. 7 cm
         d. 12 cm
    
    Jawab
    
    a. Luas permukaan $=6 \times s^2=6 \times 4^2=96$ cm$^2$
    b. Luas permukaan $=6 \times s^2=6 \times 10^2=600$ cm$^2$
    c. Luas permukaan $=6 \times s^2=6 \times 7^2=294$ cm$^2$
    d. Luas permukaan $=6 \times s^2=6 \times 12^2=864$ cm$^2$
    
    
    
21. Sebuah benda berbentuk kubus luas permukaannya 1.176 cm$^2$ . Berapa panjang rusuk kubus itu?
    
    Jawab
    
    rusuk kubus $\displaystyle =\sqrt {\frac {Luas}{6}}=\sqrt {\frac {1176}{6}}=14$ cm
    
    
22. Dua buah kubus masing-masing panjang rusuknya 6 cm dan 10 cm. Hitunglah perbandingan luas permukaan dua kubus tersebut.
    
    Jawab
    
    Luas kubus 1 : Luas kubus 2 $=6\times s_1^2 : 6\times s_2^2$
    
                                             $=6\times 6^2 : 6\times 10^2$
    
                                             $= 9 : 25$
      
    
    
23. Hitunglah luas permukaan balok dengan ukuran sebagai berikut.
         a. $8 \times 4 \times 2 $ cm
         b. $8 \times 3 \times 4 $ cm
         c. $9 \times 9 \times 6 $ cm
         d. $9 \times 8 \times 4 $ cm
    
    Jawab
         a. Luas permukaan $= 2\times (p\times l+p\times t+l\times t)$
                                        $=2 \times (8 \times 4+8\times 2 + 4\times 2)$
                                        $=2\times (32 +16+8)=2\times 56=112 $ cm$^2$
    
         b. Luas permukaan $= 2\times (p\times l+p\times t+l\times t)$
                                        $=2 \times (8 \times 3+8\times 4 + 3\times 4)$
                                        $=2\times (24 +32+12)=2\times 68=136 $ cm$^2$
    
         c. Luas permukaan $= 2\times (p\times l+p\times t+l\times t)$
                                        $=2 \times (9 \times 9+9\times 6 + 9\times 6)$
                                        $=2\times (81 +54+54)=2\times 189=378 $ cm$^2$
    
         d. Luas permukaan $= 2\times (p\times l+p\times t+l\times t)$
                                        $=2 \times (9 \times 8+9\times 4 + 8\times 4)$
                                        $=2\times (72 +36+32)=2\times 140=280 $ cm$^2$
    
    
    
24. Suatu balok memiliki luas permukaan 198 cm$^2$ . Jika lebar dan tinggi balok masing-masing 6 cm dan 3 cm, tentukan panjang balok tersebut.
    
    Jawab
    
             Luas permukaan $= 2\times (p\times l+p\times t+l\times t)$
                      198            $=2 \times (p \times 6+p\times 3 + 6\times 3)$
                      198            $=2\times (6p +3p+18)$
                      198            $= 18p+36$
    
             $\Leftrightarrow$     $\displaystyle p=\frac {198-36}{18}=\frac {162}{18}=9$ cm
    
    
25. Hitunglah perbandingan luas permukaan dua buah balok yang berukuran $(6 \times 5 \times 4)$ cm dan $(8 \times 7 \times 4)$ cm.
    
    Luas balok 1 : Luas balok 2 $=2\times (p_1\times l_1+p_1\times t_1 +l_1 \times t_1) : 2\times (p_2\times l_2+p_2\times t_2 +l_2 \times t_2)$ 
    
    Luas balok 1 : Luas balok 2 $=2\times (6\times 5+6\times 4 +5 \times 4) : 2\times (8\times 7+8\times 4 +7 \times 4)$ 
    
    Luas balok 1 : Luas balok 2 $=(30+24+20) :  (56+32 +28)$ 
    
    Luas balok 1 : Luas balok 2 $=74 :  116$
    
    Luas balok 1 : Luas balok 2 $=37 :  58$ 

Jawaban soal perbandingan dan skala kelas 7

    A.  Pilihan Ganda

Berilah tanda silang(x) pada huruf   a, b, c, atau d di depan jawaban yang tepat!

1. Setiap   minggu  4.  ekor  sapi  dapat   menghabiskan  16 karung  rumput  teki Jika  ayah mempunyai   9 ekor  sapi,  maka  banyaknya rumput teki yang diperlukan   ayah adalah…karung

   a. 30 b.      33 c.       36 d.      39

   Pembahasan Misalkan a : jumlah sapi mula-mula = 4 ekor sapi b : jumlah rumput untuk 4 ekor sapi = 16 karung p : jumlah sapi ayah = 9 ekor sapi q : jumlah rumput untuk 9 ekor sapi = ? karung
   Karena jenisnya adalah perbandingan senilai maka berlaku rumus $\displaystyle \frac{a}{b}=\frac{p}{q}$ $\Leftrightarrow$ $\displaystyle \frac{4}{16}=\frac{9}{q}$ $\Leftrightarrow$ $\displaystyle q=\frac{16\times 9}{4}=36$ jadi jumlah rumput yang dibutuhkan = 36 karung Jawaban c
2. Pada suatu  daerah  pada gambar  menggunakan  skala  1 :  11.000.000.   Jika jarak  antara dua kota pada peta adalah   6 cm,  maka jarak  sebenarnya   antara  dua  kota  adalah  ...Km
   a. 66                  b. 660 c.       6.600 d.  66.000 Pembahasan Jarak Peta (JP) = 6 cm Perbandingan = 1 : 11.000.000 $\displaystyle =\frac {1}{11.000.000}$ Jarak sebenarnya (JP) = ? Rumus : Skala $= \displaystyle \frac {JS}{JP}$ $\Leftrightarrow$ $\displaystyle \frac {1}{11.000.000} = \frac {6}{JS}$ $\Leftrightarrow$ $\displaystyle JS \times 1 = 6 \times 11.000.000$ $\Leftrightarrow$ $\displaystyle JS = 66.000.000$ cm = 660 km. Jawaban b
3.  Skala dari suatu gambar rencana pembangunan gedung  adalah 1: 200. Jika tinggi gedung pada gambar rencana adalah12,5 cm. Maka jarak sebenarnya adalah... m
             a.    16 b.    25 c.    30 d. 35 
   
   Pembahasan Jarak Peta (JP) = 12,5 cm Perbandingan = 1 : 200 $\displaystyle ='frac {1}{200}$ Jarak sebenarnya (JP) = ? Rumus : Skala $= \displaystyle \frac {JS}{JP}$ $\Leftrightarrow$ $\displaystyle \frac {1}{200} = \frac {12,5}{JS}$ $\Leftrightarrow$ $\displaystyle JS \times 1 = 12,5 \times 200$ $\Leftrightarrow$ $\displaystyle JS = 2500$ cm = 25 m. Jawaban b
   
4. Sebuah mobil rnenqhabiskan 8 liter bensin untuk menempuh jarak 56 km. Jika jarak yang ditempuh 84 km, maka bensin yang diperlukan adalah...
   a. 5,5 liter b. 7,0 liter c. 10,5 liter d. 12,0 liter

   Pembahasan Misalkan a : jumlah bensin untuk 56 km = 8 liter b : jarak mula-mula = 56 km p : jumlah bensin untuk 84 km = ? liter q : jarak yang akan ditempuh = 84 km

   Karena jenisnya adalah perbandingan senilai maka berlaku rumus $\displaystyle \frac{a}{b}=\frac{p}{q}$ $\Leftrightarrow$ $\displaystyle \frac{8}{56}=\frac{p}{84}$ $\Leftrightarrow$ $\displaystyle p=\frac{8\times 84}{56}=\frac {8 \times 3}{2}=12 $ liter jadi jumlah bensin yang dibutuhkan untuk menempuh jarak 84 km = 12 liter jawaban d
5. Sebuah panti asuhan memiliki persediaan beras yang cukup untuk 20 orang selama 15 hari. Jika penghuni panti asuhan bertambah 5 orang,  persediaan beras akan habis dalam waktu … a. 8 hari b.      10 Hari c.       12 Hari d.      20 Hari
   Pembahasan Misalkan a : jumlah anak panti mula-mula = 20 orang b : Jumlah hari dimana beras habis untuk jumlah anak panti mula-mula = 15 hari p : jumlah anak panti kemudian = 20 + 5 = 25 orang q : jumlah hari dimana beras akan habis untuk jumlah anak panti kemudian = ? hari
   Karena jenisnya adalah perbandingan berbalik nilai maka berlaku rumus $\displaystyle a \times b = p \times q $ $\Leftrightarrow$ $\displaystyle 20 \times 15= 25 \times q$ $\Leftrightarrow$ $\displaystyle q=\frac{20\times 15}{25}=12 $ jadi jumlah hari dimana beras panti akan habis untuk 25 anak = 12 hari jawaban c
6. Enam tahun yang lalu, jumlah umur Andi dan ibunya adalah 60 tahun dengan perbandingan   5:7.   Umur   Andi   sekarang adalah...   a.       25 tahun b.      31 tahun c.       32 tahun d.      35 tahun Pembahasan
   Misalkan a : umur Andi 6 tahun yang lalu b : umur Ibu 6 tahun yang lalu perbandingan : $a : b : a+b = 5 : 7 : (5+7)$ $\Leftrightarrow$ $a : b : a+b = 5 : 7 : (5+7)$ $\Leftrightarrow$ $a : b : 60 = 5 : 7 : 12$ $\Leftrightarrow$ $a : 60 = 5 : 12$ $\Leftrightarrow$ $\displaystyle a =\frac {5 \times 60 }{12} =25$ dengan demikian umur Andi saat ini = 12 + 6 = 31 tahun Jawaban b
7. Setiap minggu 5 ekor sapi dapat menghabiskan 15 karung rumput teki.  Jika ayah mempunyai 12 ekor sapi maka banyak rumput teki yang diperlukan ayah adalah....   a.    36 karung b.   25 karung c.       30 karung           d.      21 karung.
   Pembahasan Misalkan a : jumlah sapi mula-mula = 5 ekor sapi b : jumlah rumput untuk 4 ekor sapi = 15 karung p : jumlah sapi ayah = 12 ekor sapi q : jumlah rumput untuk 9 ekor sapi = ? karung
   Karena jenisnya adalah perbandingan senilai maka berlaku rumus $\displaystyle \frac{a}{b}=\frac{p}{q}$ $\Leftrightarrow$ $\displaystyle \frac{5}{15}=\frac{12}{q}$ $\Leftrightarrow$ $\displaystyle q=\frac{15\times 12}{5}=36$ jadi jumlah rumput yang dibutuhkan = 36 karung Jawaban a
8. Tono memiliki 18 kelereng dan Budi memiliki 12 kelereng. perbandingan banyak kelereng Tono dan Budi adalah... a. 3 : 2 b.      2 : 3 c.       9 : 3 d.      3 : 9 Pembahasan Misalkan T = jumlah kelereng Tono = 18 B = jumlah kelereng Budi = 12 maka $\displaystyle \frac{T}{B}=\frac{18}{12}=\frac{3}{2}$ Dengan demikian perbandingan kelereng Tono dan Budi adalah 3 : 2 jawaban a
9. Perbandingan kelereng Tono dan Budi adalah 3 : 2. Jika banyaknya kelereng Tono 24 kelereng maka banyak kelereng budi adalah.... a.       14 b.      15 c. 16 d.  18 Pembahasan Misalkan T = jumlah kelereng Tono = 24 B = jumlah kelereng Budi = ? T : B = 3 : 2 = $\displaystyle \frac{3}{2}$ karena jenisnya adalah perbandingan senilai maka $\displaystyle \frac{3}{2} = \frac {T}{B}$ $\displaystyle \frac{3}{2} = \frac {24}{B}$ $\displaystyle B = \frac {24\times 2}{3}=16$ jadi jumlah kelereng Budi = 16 jawaban c
10. Perbandingan kelereng Tono dan Budi adalah 3 : 2 . Jika jumlah kelereng mereka adalah 40 kelereng maka selisih kelereng mereka adalah... a.       7 kelereng b.  8 kelereng       c.       9 kelereng d.  10 kelereng Pembahasan Misalkan T = jumlah kelereng Tono B = jumlah kelereng Budi T : B : T+B : T - B = 3 : 2 : (3 + 2) : (3 - 2) = 3 : 2 : 5 : 1 Jadi perbandingan jumlah dan selidihkelereng mereka adalah T+B : T - B = 5 : 1 40 : T - B = 5 : 1 $\displaystyle \frac{40}{T-B} = \frac {5}{1}$ $\displaystyle T-B = \frac {40\times 1}{5}=8$ jadi selisih kelereng Tono dan Budi = 8 jawaban b
11. Suatu daerah jika digambar pada skala 1 : 12.000.000. Jika jarak pada peta adalah 7 cm maka jarak sebenarnya antara 2 kota tersebut adalah ...   a.       960 km  b.      800 km c.       840 km               d.      720 km Pembahasan Jarak Peta (JP) = 7 cm Perbandingan = 1 : 12.000.000 $\displaystyle =\frac {1}{12.000.000}$ Jarak sebenarnya (JP) = ? Rumus : Skala $= \displaystyle \frac {JS}{JP}$ $\Leftrightarrow$ $\displaystyle \frac {1}{12.000.000} = \frac {7}{JS}$ $\Leftrightarrow$ $\displaystyle JS \times 1 = 7 \times 12.000.000$ $\Leftrightarrow$ $\displaystyle JS = 84.000.000$ cm = 840 km. Jawaban c
12. Skala dari suatu gambar rencana 1 : 400. Jika tinggi gedung pada gambar adalah 8 cm maka tinggi gedung sebenarnya....   a.       42 m               b.      32 m c.       36 m                  d.      30 m Pembahasan Jarak Peta (JP) = 8 cm Perbandingan = 1 : 400 $\displaystyle =\frac {1}{400}$ Jarak sebenarnya (JP) = ? Rumus : Skala $= \displaystyle \frac {JS}{JP}$ $\Leftrightarrow$ $\displaystyle \frac {1}{400} = \frac {8}{JS}$ $\Leftrightarrow$ $\displaystyle JS \times 1 = 8 \times 400$ $\Leftrightarrow$ $\displaystyle JS = 3.200$ cm = 32 m. Jawaban b
13. Sebuah mobil menghabiskan 4 liter bensin untuk menempuh 28 km. Jika jarak yang ditempuh 42  km maka bensin yang diperlukan adalah....   a.        3 liter             b.      6 liter c.       5 liter                d.      8 liter
    Pembahasan Misalkan a : jumlah bensin untuk 28 km = 4 liter b : jarak mula-mula = 28 km p : jumlah bensin untuk 84 km = ? liter q : jarak yang akan ditempuh = 42 km
    Karena jenisnya adalah perbandingan senilai maka berlaku rumus $\displaystyle \frac{a}{b}=\frac{p}{q}$ $\Leftrightarrow$ $\displaystyle \frac{4}{28}=\frac{p}{42}$ $\Leftrightarrow$ $\displaystyle p=\frac{4\times 42}{28}=\frac {42}{7}= 6 $ liter jadi jumlah bensin yang dibutuhkan untuk menempuh jarak 84 km = 6 liter jawaban b
14. Sebuah panti asuhan memiliki persediaan beras yang cukup untuk 30 orang selama 20 hari.  Jika penghuni panti asuhan bertambah 10 orang maka persediaan akan habis dalam berapa hari.... a.       10 hari b.      13 hari c.       12 hari                d.      15 hari
    Pembahasan Misalkan a : jumlah anak panti mula-mula = 30 orang b : Jumlah hari dimana beras habis untuk jumlah anak panti mula-mula = 20 hari p : jumlah anak panti kemudian = 30 + 10 = 40 orang q : jumlah hari dimana beras akan habis untuk jumlah anak panti kemudian = ? hari
    Karena jenisnya adalah perbandingan berbalik nilai maka berlaku rumus $\displaystyle a \times b = p \times q $ $\Leftrightarrow$ $\displaystyle 30 \times 20= 40 \times q$ $\Leftrightarrow$ $\displaystyle q=\frac{30\times 20}{40}==15 $ jadi jumlah hari dimana beras panti akan habis untuk 25 anak = 15 hari jawaban c
15. 5 tahun yang lalu jumlah umur Iva dan Ayahnya  adalah 70.  Dengan perbandingan 2 : 5.  Umur iva sekarang adalah....   a.       20 tahun  b.      30 tahun c.       25 tahun         d.      35 tahun Pembahasan
    Misalkan a : umur Iva 5 tahun yang lalu b : umur Ayah Iva 5 tahun yang lalu perbandingan : $a : b : a+b = 2 : 5 : (2+5)$ $\Leftrightarrow$ $a : b : a+b = 2 : 5 : 7$ $\Leftrightarrow$ $a : b : 70 = 2 : 5 : 7$ $\Leftrightarrow$ $a : 70 = 2 : 7$ $\Leftrightarrow$ $\displaystyle a =\frac {2 \times 70 }{7} =20$ dengan demikian umur Andi saat ini = 20 + 5 = 25 tahun Jawaban c
16. Perbandingan uang Nadia: Alia: Sunan = 2: 3 : 5. Jika selisih uang Nadia dan Alia adalah 25.000. maka jumlah uang Nadia dan Alia adalah ....   a.       50.000 b.      125.000 c.       75.000                d.      150.000 Pembahasan
    Misalkan a = uang Nadia b = uang Alia c = uang Sunan perbandingan : $a : b : c : b-a : a + b = 2 : 3 : 5 : (3-2) : (2+3)$ $\Leftrightarrow$ $a : b : c : b-a : a + b + c = 2 : 3 : 5 : 1 : 5$ Jadi perbandingan selisih uang Nadia dan Alia dengan jumlah uang mereka adalah $\Leftrightarrow$ $b-a : a + b = 1 : 5$ $\Leftrightarrow$ $25000 : a+b = 1 : 5$ $\Leftrightarrow$ $\displaystyle a+b =\frac {25.000 \times 5 }{1} =125.000$ dengan demikian jumlah uang mereka = 125.000 Jawaban b
17. Perbandingan Uang Maman , Nunung, dan Opik adalah 3 : 7 : 4. Jika jumlah uang ketiganya adalah Rp 280.000,00. Tentukan jumlah uang Maman dan Opik.   a.       150.000 b.      140.000 c.       130.000 d.      120.000 Pembahasan
    Misalkan a = uang Maman b = uang Nunung c = uang Opik perbandingan : $a : b : c : a+c : a + b + c = 3 : 7 : 4 : (3+4) : (3+7+4)$ $\Leftrightarrow$ $a : b : c : a+c : a + b + c = 3 : 7 : 4 : 7 : 14$ Jadi perbandingan jumlah uang Maman dan Opik dengan jumlah uang mereka adalah $\Leftrightarrow$ $a+c : a + b + c = 7 : 14$ $\Leftrightarrow$ $a+c : 280.000 = 7 : 14$ $\Leftrightarrow$ $\displaystyle a+c =\frac {280.000 \times 7 }{14} =140.000$ dengan demikian jumlah uang mereka = 140.000 Jawaban d
18. Gambar sebidang tanah berbentuk persegi panjang berskala 1 : 400. Jika panjang dan lebar gambar 3 cm dan 5 cm . maka luas sebenarnya adalah   a.       240 m$^2$          b.      300m$^2$ c.       260 m$^2$          d.      360 m$^2$
    
    cara I Jarak Peta ($l = JP_1$) = 3 cm Jarak Peta ($p = JP_2$) = 5 cm Perbandingan = 1 : 400 $\displaystyle =\frac {1}{400}$ Jarak sebenarnya (JP) = ? Rumus : Skala $= \displaystyle \frac {JS_1}{JP}$ $\Leftrightarrow$ $\displaystyle \frac {1}{400} = \frac {3}{JS_1}$ $\Leftrightarrow$ $\displaystyle JS \times 1 = 3 \times 400$ $\Leftrightarrow$ $\displaystyle JS = 1.200$ cm = 12 m. Rumus : Skala $= \displaystyle \frac {JS_2}{JP}$ $\Leftrightarrow$ $\displaystyle \frac {1}{400} = \frac {5}{JS_2}$ $\Leftrightarrow$ $\displaystyle JS \times 1 = 5 \times 400$ $\Leftrightarrow$ $\displaystyle JS = 2.000$ cm = 20 m. jadi luas daerah sebenarnya $p\times l =12\times 20=240$ m$^2$ cara II Jika diketahui sebuah peta dengan ukuran $p \times l$ dan skala = 1 : a, maka luas daerah sesunggungnya akan memiliki skala 1 : a^2 pada soal jarak peta $(l=JP_1) = 3$ cm jarak peta $(p=JP_2) = 5$ cm
    luas gambar (LP)  $=p\times l = 3\times 5 =15$ cm$^2$
    luas sebenarnya (LS) = ?
    
    skala jarak = 1 : 400     maka skala luas $=1 : 400^2=1:160.000$
    jadi skala luas $\displaystyle =\frac{LP}{LS}$ $\Leftrightarrow$ $\displaystyle \frac{1}{160.000}=\frac{15}{LS}$
    $\Leftrightarrow$ $\displaystyle LS=15 \times 160.000=2.400.000$ cm$^2$ =240 m$^2$.
    Jadi luas sebenarnya $=240$ m$^2$ Jawaban a
19. Seorang siswa membuat denah sebuah gedung berikut pekarangannnya pada kertas gambar berukuran 40 x 30 cm . Ukuran gedung tersebut sebenarnya adalah  200m x 150 m. Skala yang mungkin adalah... a.       1:200              b. 1:400 c. 1:300              d. 1: 500 pembahasan cara 1 Jarak sebenarnya untuk panjang ($JS_1$) = 200 m = 20.000 cm ukuran kertas gambar untuk panjang ($JP_1$) = 40 cm Jarak sebenarnya untuk lebar ($JS_2$) = 150 m = 15.000 cm Jarak kertas gambar untuk lebar ($JP_2$) = 30 cm perbandingan panjang untuk peta dengan ukuran panjang sebenarnya $\displaystyle =\frac{JP_1}{JS_1}=\frac{40}{20.000}=\frac{1}{500}=1:500$ perbandingan panjang untuk peta dengan ukuran panjang sebenarnya $\displaystyle =\frac{JP_2}{JS_2}=\frac{30}{15.000}=\frac{1}{500}=1:500$ karena kedua perbandingan tersebut sama, maka skala maksimal yang mungkin adalah 1 : 500 cara 2 Luas kertas $ LP= 40\times 30 = 1200$ cm$^2$ Luas sesungguhnya $LS=20.000 \times 15.000 =300.000.000$ cm$^2$ maka skala yang mungkin adalah $\displaystyle \sqrt {\frac{LP}{LS}}=\sqrt {\frac{1200}{300.000.000}} =\sqrt {\frac{1}{250.000}}=\frac{1}{500}=1:500$ jawaban d
20. Pak Ardi membuat denah gedung pada kertas berukuran 40 cm x 30 cm. Jika ukuran gedungnya 28 m x 21 m maka skala yang mungkin adalah...   a.   1: 50               b. 1: 70 c. 1: 60               d. 1:65 pembahasan cara I Jarak sebenarnya untuk panjang ($JS_1$) = 28 m = 2800 cm ukuran kertas gambar untuk panjang ($JP_1$) = 40 cm Jarak sebenarnya untuk lebar ($JS_2$) = 21 m = 2100 cm Jarak kertas gambar untuk lebar ($JP_2$) = 30 cm perbandingan panjang untuk peta dengan ukuran panjang sebenarnya $\displaystyle =\frac{JP_1}{JS_1}=\frac{40}{2800}=\frac{1}{70}=1:70$ perbandingan panjang untuk peta dengan ukuran panjang sebenarnya $\displaystyle =\frac{JP_2}{JS_2}=\frac{30}{2100}=\frac{1}{70}=1:70$ karena kedua perbandingan tersebut sama, maka skala maksimal yang mungkin adalah 1 : 70 cara 2 Luas kertas $ LP= 40\times 30 = 1200$ cm$^2$ Luas sesungguhnya $LS=2.800 \times 2.100 =5.880.000$ cm$^2$ maka skala yang mungkin adalah $\displaystyle \sqrt {\frac{LP}{LS}}=\sqrt {\frac{1200}{5.880.000}} =\sqrt {\frac{1}{4.900}}=\frac{1}{70}=1:70$ jawaban d
21. Sebuah mobil memerlukan 5 liter bensin untuk menempuh jarak 25 km. Jika ternyata mobil menghabiskan 7 liter bensin maka jarak yang ditempuh adalah.... a. 35 km             b. 45 km c. 40 km           d. 50 km
    Pembahasan Misalkan a : jumlah bensin untuk 25 km = 5 liter b : jarak mula-mula = 25 km p : jumlah bensin untuk 84 km = 7 liter q : jarak yang akan ditempuh = ? km
    Karena jenisnya adalah perbandingan senilai maka berlaku rumus $\displaystyle \frac{a}{b}=\frac{p}{q}$ $\Leftrightarrow$ $\displaystyle \frac{5}{25}=\frac{7}{q}$ $\Leftrightarrow$ $\displaystyle q=\frac{25\times 7}{5}=5 \times 7=35 $ km jadi bensin 7 liter dapat digunakan untuk menempuh jarak 35 km jawaban a
22. Pada sebuah acara diperlukan 200 loyang kue untuk menjamu 800 orang. Banyak kue yang dibutuhkan untuk menjamu 1200 orang adalah... a.       250                 b.      420 c.       300                 d.      460
    Pembahasan Misalkan a : jumlah kue mula-mula = 200 loyang b : jumlah orang mula-mula = 800 orang p : jumlah kue yang dibutuhkan = ? liter q : jumlah orang yang hadir = 1200 orang
    Karena jenisnya adalah perbandingan senilai maka berlaku rumus $\displaystyle \frac{a}{b}=\frac{p}{q}$ $\Leftrightarrow$ $\displaystyle \frac{200}{800}=\frac{p}{1200}$ $\Leftrightarrow$ $\displaystyle p=\frac{200\times 1200}{800}=\frac {1200}{4}=300 $ liter jadi jumlah kue yang dibutuhkan untuk 1200 orang adalah 300 loyang jawaban c
23. Persediaan pakan ternak 100 ayam cukup untuk 36 hari. Jika ayam bertambah 20 ekor maka makanan akan cukup dalam berapa hari...   a.  26 hari                 b.  40 hari c. 30 hari            d. 50 hari
    Pembahasan Misalkan a : jumlah ayam mula-mula = 100 ekor b : jumlah hari dimana pakan habis untuk 100 ayam = 36 hari p : jumlah ayam kemudian = 100+20=120 ekor q : jumlah hari pakan akan habis untuk 120 ayam = ? hari
    Karena jenisnya adalah perbandingan berbalik nilai maka berlaku rumus $\displaystyle a\times b= p\times q$ $\Leftrightarrow$ $\displaystyle 100\times 36=120\times q$ $\Leftrightarrow$ $\displaystyle q=\frac{100\times 36}{120}=30 $ hari jadi pakan akan habis dalam waktu 30 hari jawaban c
24. Bu Beni membeli 4 baju dengan harga Rp 220 000,00. Bila Bu Lia akan membeli 8 baju sama ditempat yang sama maka Bu lia harus membayar ....   a.  440.000          b. 110.000 c. 660.000          d. 220.000
    Pembahasan Misalkan a : harga 4 baju yang dibeli Bu Beni= 220.000,00 b : jumlah baju yang dibeli Bu Beni = 4 buah p : harga baju yang hendak dibayar Bu Lia = ? liter q : Jumlah baju yang dibeli Bu Lia = 8 buah
    Karena jenisnya adalah perbandingan senilai maka berlaku rumus $\displaystyle \frac{a}{b}=\frac{p}{q}$ $\Leftrightarrow$ $\displaystyle \frac{220.000}{4}=\frac{p}{8}$ $\Leftrightarrow$ $\displaystyle p=\frac{220.000\times 8}{4}=220.000 \times 2= 440.000 $ jadi harga 8 baju yang harus dibayar Bu Lia Rp. 440.000,00 jawaban a
25. Sebuah pekerjaan dapat diselesaikan 6 hari oleh 5 orang pekerja. Pekerjaan itu ternyata dikerjakan 10 orang maka akan selesai .... hari   a.  3 hari   b. 2 hari c.  5 hari     d.  6 hari
    Pembahasan
    
    Karena jenisnya adalah perbandingan berbalik nilai maka berlaku rumus $\displaystyle a \times b=p \times q$ $\Leftrightarrow$ $\displaystyle 6 \times 5 = p\times 10$ $\Leftrightarrow$ $\displaystyle p=\frac{6\times 5}{10}=\frac {30}{10}=3 $ hari jadi 10 orang akan dapat menyelesaikan pekerjaan dalam 3 hari jawaban a
    = Selamat Mengerjakan =

    NB: Untuk materinya, kalian bisa baca di tautan : "Perbandingan dan Skala"

Pembahasan latihan soal kelas VII: Hubungan titik dengan garis dan bidang

  Kerjakanlah soal berikut dengan baik dan benar

1. Bagaimana keberadaan titik dengan garis, titik dengan bidang,? Jelaskan!
    
   Jawab
   
   Titik dengan  garis
   ada 2 kemungkinan hubungan titik dengan garis yakni titik pada garis dan titik diluar garis. Titik pada garis berarti titik tersebut terletak pada sebuah garis, Sebaliknya, titik diluar garis berarti titik tersebut tidak berada pada garis yang dimaksudkan
   
   Titik dengan  bidang
   Sebuah titik atau lebih dapat terletak pada suatu bidang. Jika titik terletak pada sebuah bidang maka titik tersebut menjadi bagian dari bidang yang dimaksudkan. Kemungkinan yang lain, titik bisa terletak di luar bidang apabila titik tersebut bukan dari bidang yang bersangkutan.  Titik-titik yang terletak pada bidang yang sama memiliki hubungan titik-titik sebidang.
   
   
2. Sebuah garis dan bidang tidak terletak pada bidang yang sama dan tidak berpotongan, maka irisan keduanya menghasilkan,
   a. sebuah titik                                                   c. tak hingga titik
   b. dua titik                                                        d. himpunan kosong
    
   Jawab
   jika sebuah garis dan bidang tidak terleak pada bidang yang sama dan tidak berpotongan, maka irisan keduanya menghasilkan himpunan kosong
   
   
3. Terdapat dua bidang saling berpotongan dan tidak berhimpitan, maka perpotongannya berbentuk,
   a. titik                                                                c. bidang
   b. garis                                                              d. ruang
   
   Jawab
   Dua buah bidang yang saling berpotongan akan membentuk garis potong pada daerah perpotongannya
   
   
4. Perhatikan gambar berikut ini !
   
   
   

   
   
   
   a. Apakah titik P terletak pada garis $\overline {AD}$?
   b. Sebutkan titik-titik yang terletak pada garis $\overline {AD}$!
   c. Sebutkan titik-titik yang terletak di luar garis $\overline {AD}$!
   d. Pada gambar tersebut, ada berapa segmen garis yang dapat dibentuk dari garis $\overline {AD}$?
   e. Apakah titik C berada pada sinar garis $\overrightarrow {BA}$?
   f. Apakah titik D berada pada sinar garis berada pada sinar garis $\overrightarrow {AB}$ 
   
   jawab
   a, Jika kita amati, garis $\overline {AD}$ mengarah ke titik P (arahnya ditandai dengan garis putus-putus berwarna biru). Karena sifat garis tidak memiliki titik ujung, maka titik P juga terletak pada gari $\overline {AD}$.
   
   b. Titik-titik yang terletak pada garis AD adalah titik A, B, C, D dan P.
   
   c. Titik-titik yang terletak di luar garis AD adalah titik Q dan R,
   
   d. Segmen garis yang bisa dibentuk adalah $ \overline {AB}, \overline {AC},  \overline {AD}, , \overline {AP},  \overline {BC}, \overline {BD}, \overline {BP},  \overline {CD}, \overline {CP}, \overline {DP}$. Jadi ada 10 buah segmen garis yang bisa dibentuk
   
   e. Pada sinar garis $\overrightarrow {BA}$ titik pangkalnya terletak pada titik B. Dengan demikian titik C berada diluar sinar garis $\overrightarrow {BA}$.
   
   f. Pada sinar garis $\overrightarrow {AB}$ titik pangkalnya terletak pada titik A dan menuju lurus melewati titik B lalu kemudian melewati C dan D dan terus sampai tak berkesudahan. Dengan demikian titik D berada pada sinar garis $\overrightarrow {AB}$..
    
5. Pada kubus ABCD.EFGH buatlah bidang menurut ketentuan sebagai berikut :
   a. Melalui titik B, D dan titik G.
       Periksalah, apakah titik A dan H berada pada bidang tersebut!
   
      jawab: Perhatikan gambar berikut
   
   
   
   
      Pada gambar nampak bahwa titik A dan H terletak di luar bidang BDG
   
   b. Melalui titik A, C dan titik G
       Periksalah, apakah titik E dan B terletak pada bidang ACG?
   
       Jawab: Perhatikan gambar berikut:
   
   
   
       
   Bidang ACG masih terletak satu bidang dengan bidang diagonal ACGE. Dengan demikian titik E masih terletak pada bidang ACG. Sementara titik B terletak diluar bidang ACG.
   
   
   
   ---- Selamat Belajar kembali!  ----

 

Join together with Altissima Study Center
By
Subscribe and like this channel,

give positive comment

support our efforts and hard work,

If you want to contact us, please send your email at altissimastudycenter@gmail.com