Tampilkan postingan dengan label Pembahasan VIII. Tampilkan semua postingan

Rabu, 02 Februari 2022

Pembahasan Soal Ulangan harian : Balok dan Kubus

Ulangan Harian Matematika

Kelas 8 SMP

Materi : Kubus dan Balok

============ 000 ===========

Kerjakan soal berikut dengan baik dan benar

A. Soal Pilihan Ganda

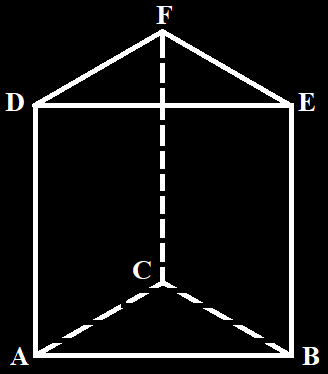
Perhatikan gambar berikut ini

Pernyataan di bawah ini benar, kecuali ....
a. AB // DC // EF // HG
b. AE // BF // CG // DH
c. AD // EH // BC // FG
d. AD // BC // BF // CG

jawab:

Jawaban d. karena garis AD tegak lurus dengan garis BF tetapi AD sejajar dengan BC dan bersilangan dengan CG
Perhatikan gambar berikut ini:

Jika rangkaian persegi panjang di atas dilihat sepanjang garis putus-putus, akan terbentuk bangun ....
a. kubus
b. prisma
c. limas
d. balok

Jawab

Gambar tersebut merupakan jaring-jaring balok
Sebuah balok mempunyai luas permukaan 376 cm$^2$. Jika panjang balok 10 cm, lebar balok 6 cm, tinggi balok adalah ....
a. 6 cm
b. 8 cm
c. 7 cm
d. 9 cm

jawab

Luas permukaan balok $=2\times (p\times l+p\times t + l \times t)$
376 $= 2\times (10 \times 6 + 10 \times t + 6\times t)$

$\displaystyle \frac {376}{2}$ $=60 +(10+6) \times t$

188 = 60 + 16 t

$\Leftrightarrow$ $\displaystyle t=\frac{188-60}{16}=\frac{128}{16}=8$ cm
Sebuah kubus panjang rusuknya 6 cm. Luas permukaan kubus itu adalah ....
a. 36 cm$^2$
b. 432 cm$^2$
c. 216 cm$^2$
d. 1.296 cm$^2$

jawab

luas permukaan kubus $=6\times s^2=6\times 6^2=216$ cm$^2$
Pernyataan di bawah ini yang benar adalah ....
a. Dua garis dalam ruang dikatakan bersilangan jika kedua garis itu tidak berpotongan dan
terletak pada satu bidang.
b. Sebuah balok memiliki enam diagonal ruang.
c. Sebuah balok memiliki enam bidang diagonal yang berbentuk persegi panjang dan
sepasang-sepasang kongruen.
d. Diagonal bidang balok adalah ruas garis yang menghubungkan dua titik sudut yang saling
berhadapan dalam ruang pada kotak.

jawab
Pernyataan (a) salah karena dua buah garis yang bersilangan terletak pada bidang yang berbeda
Pernyataan (b) salah karena balok memiliki 4 diagonal ruang
Pernyataan (d) salah karena diagonal bidang merupakan ruas garis yang menghubungkan dua titik sudut yang saling berhadapan pada permukaan bidang datar balok.
Selisih panjang rusuk dua buah kubus adalah 3 dm. Jika selisih luas sisi kubus itu 234 dm2, selisih volume kedua kubus adalah ....
a. 358 dm$^3$
b. 387 dm$^3$
c. 378 dm$^3$
d. 387,5 dm$^3$

Misalkan R dan r masing-masing merupakan rusuk kubus 1 dan kubus 2, .maka

R - r = 3 dm dan $6R^2 - 6r^2 =234$ dm$^2$

$\displaystyle R^2 - r^2 =\frac {234}{6}=39$

dengan mensubtitusikan kedua persamaan di atas didapat

$R^2 - r^2 = 39$
$(R - r)(R + r) = 39$
$3 (R + r) = 39$
$\displaystyle R + r =\frac{39}{3} = 13$

Oleh karena itu didapat

$R+r = 13$
$\underline {R-r = 3}$ -
$2r = 10$ $\Leftrightarrow$ $\displaystyle r =\frac{10}{2}$

$R+r = 13$
$\underline {R-r = 3}$ +
$2R = 16$ $\Leftrightarrow$ $\displaystyle R =\frac{16}{2}$

Dengan demikian selisih Volume dapat dicari yakni

Volume kubus 1 - Volume kubus 2 $\displaystyle = \left ( \frac {16}{2} \right )^3 - \left ( \frac {10}{2} \right )^3 = \frac{4096-1000}{8}=\frac{3096}{8}=387 $ dm$^3$
Rusuk-rusuk balok yang bertemu pada sebuah pojok balok berbanding 4 : 4 : 1. Jika volume balok 432 liter, luas permukaan balok adalah ....
a. 423 dm$^2$
b. 452 dm$^2$
c. 432 dm$^2$
d. 464 dm$^2$

Jawab

misalkan ukuran rusuk adalah p = 4x, l = 4x dan t = x. maka

Volume balok $=p \times l \times t = 4x \times 4x \times x $

432 $=16 \times x^3$

$\Leftrightarrow$ $\displaystyle x =\sqrt[3] {\frac{432}{16}}=\sqrt[3]{27}=3$

Dengan demikian

Luas permukaan balok $= 2\times (4x \times 4x + 4x \times x +4x\times x)$

Luas permukaan balok $= 2\times (4x \times (4x + x + x))$

Luas permukaan balok $= 2\times (4x \times 6x = 48 x^2=48 \times 3^2 = 432 $ dm$^2$
Selisih panjang rusuk dua buah kubus adalah $\displaystyle \frac {1}{2}$ m dan selisih volumenya $\displaystyle \frac{7}{8}$ m$^3$. Jika kubus besar disusun menjadi kubus-kubus kecil yang kongruen dengan panjang rusuk 10 cm, banyaknya kubus-kubus kecil itu adalah ....
a. 10 buah
b. 500 buah
c. 100 buah
d. 1.000 buah

jawab

Misalkan R = rusuk kubus besar dan r = rusuk kubus kecil

maka $\displaystyle R - r = \frac {1}{2}$ $\Leftrightarrow$ $\displaystyle r = R - \frac{1}{2}$

$\Leftrightarrow$ $\displaystyle r^3 = \left ( R - \frac{1}{2} \right )^3$ ..... persamaan 1

$\displaystyle R^3 - r^3 = \frac {7}{8}$ $\Leftrightarrow$ $r^3=R^3 - \frac{7}{8}$ ..... persamaan 2

dari persamaan 1 dan 2 diperoleh

$ \left ( R- \frac{1}{2} \right )^3 = R^3 - \frac{7}{8}$

$ R^3 + \frac{3r}{4} -\frac {3R^2}{2}-\frac {1}{8} = R^3 -\frac{7}{8}$

$ \frac{3R}{4} -\frac {3R^2}{2}-\frac {1}{8} + \frac{7}{8}= 0$

$ \frac{3R}{4} -\frac {3R^2}{2}+\frac {6}{8} = 0$ kalikan 4

$ -6R^2 +3R+ 3 = 0$ $\Leftrightarrow$ $2R^2 - r -1= 0$

$\Leftrightarrow$ $(2R + 1)(R -1)= 0$

$\Leftrightarrow$ $\displaystyle R = -\frac {1}{2}$ atau $ R = 1$

Karena ukuran jarak bernilai positif, pilih R = 1 m = 100 cm dan $\displaystyle r =R-\frac{1}{2}=\frac{1}{2}$ m $\displaystyle =\frac{1}{2}\times 100 =50$ cm . Dengan demikian jumlah kubus kecil berukuran 10 cm yang dapat mengisi kubus dengan R = 100 cm adalah :

Jumlah kubus kecil $\displaystyle = \frac{100^3}{10^3}=\left ( \frac{100}{10} \right )^3=10^3 = 1000 $ kubus
Diketahui balok ABCD.EFGH dengan AB = (x + 1) cm, BC = x cm, dan AC = (x + 2) cm. Jika tinggi balok 2 cm, volume balok adalah ....
a. 9 cm$^3$
b. 42 cm$^3$
c. 24 cm$^3$
d. 48 cm$^3$

Jawab

Dengan menggunakan rumus phytagoras diperoleh

$AB^2 + BC^2 = AC^2$

$ (x+1)^2 + x^2 = (x+2)^2$

$ x^2+2x+1 + x^2 = x^2+4x+4$

$ x^2-2x-3 =0$ $\Leftrightarrow$ $(x-3)(x+1)=0$ $\Leftrightarrow$ $x = 3$ atau $x=-1$

Pilih x = 3, didapat AB = 4, BC = 3 dan AC = 5. Dengan demikian volume balok adalah

Volume $= AB \times BC \times tinggi = 4 \times 3 \times 2 =24$ cm$^2$
Sebuah kubus memiliki rusuk sepanjang 6 cm. Rusuk itu diperpanjang sebesar k kali panjang rusuk semula, sehingga volumenya menjadi 1.728 cm3. Nilai k adalah ....
a. 2
b. 6
c. 4
d. 8

jawab

karena R = 6k, maka

Volume $=R^3$ $\Leftrightarrow$ $ 1728 =(6k)^3$

$\Leftrightarrow$ $ 1728 =216 k^3$

$\Leftrightarrow$ $ \displaystyle k =\sqrt[3]{\frac {1728}{216}}=\sqrt[3]{8}=2 $

B. Soal Essay

Jawab pertanyaan ini dengan jelas

Pada kertas berpetak, lukislah balok PQRS.TUVW dengan panjang 4 satuan, lebar 2 satuan, dan tinggi 3 satuan.
a. Lukislah semua diagonal ruangnya.
b. Ada berapa banyak diagonal bidangnya, sebutkan.

Jawab

a.

b. karena balok memiliki 6 sisi dan masing-masing sisi memiliki 2 diagonal bidang, maka
banyaknya diagonal bidang pada balok adalah $2\times 6= 12$ buah.
Hitunglah luas permukaan balok jika diketahui
a. V = 24 cm3, p = 4 cm, dan l = 3 cm;
b. V = 315 cm3, p = 9 cm, dan l = 7 cm.

Jawab:
a. Volume $=p \times l \times t$
24 $=4 \times 3 \times t$ $Leftrightarrow$ $\displaystyle t=\frac{24}{12}=2$ cm

Luas permukaan $= 2\times (p\times l +p\times t + l\times t)$
$=2\times (4\times 3+4 \times 2 +3\times 2)$
$=2\times(12+8+6)=52$ cm$^2$

b. Volume $=p \times l \times t$
315 $=9 \times 7 \times t$ $Leftrightarrow$ $\displaystyle t=\frac{315}{63}=5$ cm

Luas permukaan $= 2\times (p\times l +p\times t + l\times t)$
$=2\times (9\times 7+9 \times 5 +7\times 5)$
$=2\times(63+45+35)=286$ cm$^2$
Sebuah kubus panjang setiap rusuknya 2 m. Kubus tersebut tersusun dari kubus-kubus kecil dengan panjang setiap rusuknya 20 cm.
a. Tentukan volume kubus besar dan kubus kecil.
b. Berapa banyak kubus kecil hingga tersusun kubus besar?

jawab

a. Volume kubus besar $=200^3=8.000.000$ cm$^3$
Volume kubus kecil $=20^3=8.000$ cm$^3$

b. Banyaknya kubus kecil $\displaystyle =\frac{8.000.000}{8.000}=1.000$ buah
Luas permukaan sebuah kubus adalah 294 cm$^2$. Hitunglah
a. panjang diagonal bidangnya;
b. panjang diagonal ruangnya;
c. volume kubus.

Jawab:
Luas permukaan $ = 6 \times s^2$
294 $ = 6 \times s^2$

$\Leftrightarrow$ $\displaystyle s=\sqrt{\frac{294}{6}}=\sqrt{49}=7$ cm

a. Panjang diagonal bidang $=\sqrt{7^2+7^2}=7\sqrt 2$ cm
b. Panjang diagonal ruang $=\sqrt{7^(7\sqrt 2)^2}=7\sqrt 3$ cm
c. Volume $=s^3=7^3=343$ cm$^3$
Diketahui tempat air berukuran panjang 60 cm, lebar 50 cm, dan tinggi 100 cm berisi air penuh. Air tersebut akan dikurangi dengan cara melubangi tempat tersebut, hingga air yang keluar ditampung dalam tempat lain yang berukuran $(40 \times 30 \times 20)$ cm.
a. Tentukan volume penampungan air.
b. Tentukan tinggi permukaan air pada tempat pertama setelah dikurangi.

Jawab

a. Volume penampungan air $=40 \times 30 \times 20 =24000$ cm$^3$
b. Volume bak air $=60\times 50\times 100=300.000$ cm$^3$
Selisih volume $=300.000-24.000=276.000$ cm$^3$

tinggi air dalam bak setelah dikurangi $\displaystyle =\frac{276.000}{60\times 50}=\frac{276.000}{3000}= 92$ cm.

Selasa, 01 Februari 2022

Pembahasan Soal Bangun ruang

Kerjakan soal berikut dengan baik dan benar

Banyaknya titik sudut pada prisma segitiga adalah ....
a. 6 buah
b. 10 buah
c. 8 buah
d. 12 buah

Jawab:

Perhatikan gambar di bawah ini :

Dengan demikian nampak bahwa jumlah sudut prisma segitiga adalah 6 buah.
Banyaknya rusuk alas pada limas segi empat adalah ....
a. 3 buah
b. 7 buah
c. 4 buah
d. 8 buah
Perhatikan gambar prisma segi lima beraturan berikut ini.

Pernyataan di bawah ini benar, kecuali ....
a. rusuk-rusuk tegaknya adalah KP, LQ, MR, NS, dan OT
b. bidang KLMNO kongruen dengan bidang PQRST
c. bidang KMRP dan KNSP merupakan bidang diagonal
d. diagonal bidang alasnya ada 4 buah

Jawab :
Jawaban yang salah adalah (d) sebab jumlah diagonal alasnya adalah 5 buah. yakni: OL, OM, KM, KN, dan LN.
Gambar di bawah ini merupakan jaring - jaring ....

a. limas segi lima beraturan
b. limas segi enam beraturan
c. prisma segi lima beraturan
d. prisma segi enam beraturan

Jawab
Jika melihat segilima sebagai alasnya dan kelima segitiga sebagai sisi tegaknya, maka bangun ruang yang terbentuk adalah limas segilima beraturan.
Suatu prisma alasnya berbentuk segitiga dengan panjang sisi 3 cm, 4 cm, dan 5 cm. Jika tinggi prisma 15 cm, volume prisma adalah ....
a. 90 cm$^3$
b. 250 cm$^3$
c. 200 cm$^3$
d. 300 cm$^3$

Jawab
jika melihat ukuran panjang sisi segitiga alasnya, maka segitiga tersebut memenuhi syarat phytagoras dengan kedua sisi siku-sikunya memiliki panjang 3 cm dan 4 cm. Dengan demikian volume prisma segitiga adalah

Volume prisma = luas alas $\times$ tinggi prisma = $\displaystyle \left (\frac {1}{2} \times 3 \times 4 \right ) \times 15 = 90$ cm$^3$
Diketahui luas permukaan prisma tegak segi empat beraturan 864 cm$^2$ dan tinggi prisma 6 cm. Panjang sisi alas prisma adalah ....
a. 8 cm
b. 12 cm
c. 10 cm
d. 14 cm

Jawab
Volume prisma = luas alas $\times$ tinggi prisma = $\displaystyle s \times s \times 12 $

$\Leftrightarrow$ $\displaystyle s^2= \frac {864}{6} = 144$

$\Leftrightarrow$ $\displaystyle s= \sqrt {144}=12$ cm
Diketahui suatu limas dengan alas berbentuk persegi. Luas alas limas 144 cm2 dan tinggi limas 8 cm. Luas permukaan limas adalah ....
a. 204 cm$^2$
b. 484 cm$^2$
c. 384 cm$^2$
d. 1.152 cm$^2$

jawab

Sisi alas limas = $ \sqrt ($luas alas) $ =\sqrt {144}=12$ cm

tinggi sisi tegak limas = $\sqrt {6^2 + 8^2}=10$ cm

Dengan demikian luas permukaan limas tersebut =

Luas limas segiempat beraturan = 4 $\times$ luas segitiga + luas alas

= $\displaystyle 4 \times \frac {1}{2} \times 12 \times 10 $ + 144

= 240 + 144

= 384 cm$^2$
Diketahui volume suatu prisma 450 cm$^3$. Alas prisma berbentuk segitiga siku-siku dengan panjang sisi 5 cm, 13 cm, dan 12 cm. Tinggi prisma adalah ....
a. 12 cm
b. 14 cm
c. 13 cm
d. 15 cm

Jawab
Karena sisi terpanjang segitiga berukuran 13 cm maka sisi tegaknya berukuran 5 cm dan 12 cm

Volume Prisma = luas alas $\times$ tinggi prisma
450 $\displaystyle \frac {1}{2}\times 5 \times 12 \times$ tinggi prisma

450 $ = 30 \times$ tinggi prisma

$\Leftrightarrow$ tinggi prisma $\displaystyle =\frac {450}{30}=15$ cm
Jika suatu limas luas alasnya 240 cm$^2$ dan tinggi 30 cm maka volume limas adalah ....
a. 2.400 cm$^3$
b. 4840 cm$^3$
c. 4.400 cm$^3$
d. 7.200 cm$^3$

Jawab

Volume limas $=\displaystyle \frac {1}{3} \times$ luas alas $\times$ tinggi limas

Volume limas $=\displaystyle \frac {1}{3} \times 240 \times 30 = 2400$ cm$^3$
Suatu limas memiliki alas berbentuk persegi panjang dengan ukuran 25 cm dan 15 cm. Jika tinggi limas 7 cm, volume limas adalah ....
a. 262,5 cm$^3$
b. 870 cm$^3$
c. 484 cm$^3$
d. 875 cm$^3$

Jawab

Volume limas $=\displaystyle \frac {1}{3} \times$ luas alas $\times$ tinggi limas

Volume limas $=\displaystyle \frac {1}{3} \times 25\times 15 \times 7=875$ cm$^3$
Diketahui prisma tegak segitiga ABC.DEF dengan AB = 15 dm, BC = 12 dm, dan AC = 9 dm.

Jika tinggi prisma itu 2 dm, volumenya adalah ....
a. 108 liter
b. 540 liter
c. 216 liter
d. 1.080 liter

Jawab
alas prisma berbentuk segitiga siku-siku karena memenuhi syarat phytagoras. Dengan demikian sisi yang saling tegak lurus adalah yang berukuran 9 cm dan 12 cm.

Volume prisma = luas alas $\times$ tinggi prisma

Volume limas $\displaystyle \frac {1}{2}\times 9 \times 12 \times 2 = 108$ dm$^3 = 108$ liter
Pada prisma tegak segi empat ABCD.EFGH, sisi alas ABCD berupa trapesium sama kaki dengan AB//CD, AB = 10 cm, CD = 4 cm, dan AD = 5 cm. Jika luas semua sisi tegaknya 216 cm$^2$ maka volume prisma itu adalah ....
a. 252 cm$^3$
b. 560 cm$^3$
c. 320 cm$^3$
d. 600 cm$^3$

Jawab

Pada gambar nampak bidang ADHE sebangun dengan bidang BCGF. Dengan demikian
Luas selimut = 2 $\times$ luas ADHE + luas CDHG + luas ABFE
216 $=2 \times 5 \times$ tinggi prisma + $4 \times$ tinggi prisma + $10 \times $ tinggi prisma
216 $= (10 + 4 + 10) \times$ tinggi prisma
216 $= 24 \times$ tinggi prisma

Tinggi prisma $\displaystyle =\frac{216}{24}=9$ cm

Sekarang perhatikan $\bigtriangleup BCE$ pada trapesium ABCD seperti gambar berikut

Dengan demikian tinggi trapesium dapat kita cari dengan menggunakan phytagoras yakni

$BE =\sqrt{BC^2-EC^2}=\sqrt{5^2-3^2}=4$ cm

Volume prisma = luas alas $\times$ tinggi prisma

Volume prisma $\displaystyle =\left ( \frac{DC+AB}{2}\times BE \right ) \times 9 $

Volume prisma $\displaystyle =\left ( \frac{10+4}{2}\times 4\right ) \times 9 = 252$ cm$^3$
Diketahui limas segi empat beraturan T.ABCD, dengan AB = 8 cm dan luas bidang TAB = 24 cm$^2$. Volume limas itu adalah ...
a. 94,3 cm$^3$
b. 95,4 cm$^3$
c. 94,5 cm$^3$
d. 96 cm$^3$

Jawab
Perhatikan $\bigtriangleup TAB$ bangun ruang TABCD berikut ini

Luas $\bigtriangleup {TAB}\displaystyle =\frac {1}{2}\times AB \times tinggi_{\bigtriangleup {TAB}}$

24 $\displaystyle = \frac {1}{2} \times 8 \times tinggi_{\bigtriangleup TAB}$

24 $\displaystyle = 4 \times tinggi_{\bigtriangleup TAB}$

Tinggi$_{\bigtriangleup TAB}\displaystyle = \frac {24}{4} = 6$ cm

Sekarang perhatikan $\bigtriangleup TEO$ pada bangun ruang TABCD seperti gambar berikut

Karena EO $\displaystyle =\frac {BC}{2}=\frac {8}{2}=4$ cm dan TE = 6 cm, maka dengan menggunakan phytagoras diperoleh :

Tinggi limas $=\sqrt {TE^2-EO^2}=\sqrt {6^2-4^2}=\sqrt{20}=2\sqrt 5$

Dengan demikian kita dapat mencari volume limas, yakni :

Volume limas $\displaystyle = \frac {1}{3} \times$ luas alas $\times$ tinggi prisma

Volume limas $\displaystyle = \frac {1}{3} \times 8 \times 8 \times 2 \sqrt 5= \frac {128}{3}\sqrt 5 \approx 95,40$ cm$^3$
Alas sebuah prisma berbentuk belah ketupat, dengan salah satu panjang diagonalnya adalah 10 cm dan panjang semua sisi tegaknya adalah 12 cm. Jika volume prisma itu 600 cm3, luas sisi prisma itu adalah ....
a. $64 + 5\sqrt 2$ cm$^2$
b. $72 + 15\sqrt 2$ cm$^2$
c. $96 + 32\sqrt 2$ cm$^2$
d. $100 + 240\sqrt 2$ cm$^2$

Jawab

Volume prisma = luas alas $\times$ tinggi prisma

600 = luas alas $times 12$

Luas alas $\displaystyle = \frac {600}{12}=50$ cm$^2$

Panjang diagonal alas yang lain $\displaystyle = \frac {2 \times Luas} {diagonal}=\frac{2\times 50}{10}=10$ cm

Panjang sisi belah ketupat $=\sqrt{5^2 + 5^2}=5\sqrt 2$

luas permukaan $=2 \times$ luas alas $+ 4 \times$ luas persegi panjang

luas permukaan $=2 \times 50 + 4 \times 5 \sqrt 2 \times 12 = 100 + 240 \sqrt 2$
Sebuah prisma tegak segitiga luas bidang alasnya 24 cm$^2$ dan luas bidang sisi-sisinya adalah 150 cm$^2$, 120 cm$^2$, dan 90 cm$^2$. Volume prisma itu adalah ....
a. 90 cm$^3$
b. 220 cm$^3$
c. 120 cm$^3$
d. 360 cm$^3$

Jawab

panjang sisi segitiga alasnya masing-masing adalah 6 cm, 8 cm , dan 10 cm
(anda dipersilahkan untukk membuktikannya ya ...)

Dengan demikian tinggi prisma bisa dicari melalui salah satu sisinya. Ambil bidang yang memiliki sisi terpanjang dari segitiga alasnya dan memiliki daerah yang paling luas. Maka lebar bidang tersebut adalah 10 dan luasnya = 150 cm$^2$. Maka tinggi prisma yakni

Tinggi prisma $\displaystyle = \frac {luas}{l}=\frac {150}{10}=15$ cm

maka Volume prisma = luas alas $\times$ tinggi prisma $=24 \times 15= 360$ cm$^3$

B. Jawablah pertanyaan berikut ini!

Gambarlah prisma segi enam beraturan ABCDEF.GHIJKL. Tentukan
a. rusuk-rusuk tegaknya;
b. semua diagonal bidang alas;
c. semua diagonal ruangnya.

jawab

a. Rusuk tegak : AG, BH, CI, DJ, EK, dan FL
b. Diagonal bidang alas = AD, AE, AC, BE, BD, BF, CF, CE, dan DF

diagonal alas

c. Diagonal ruang

diagonal ruang
Limas segi empat beraturan mempunyai luas alas 256 cm$^2$. Jika tinggi limas 6 cm, tentukan luas permukaan limas tersebut.

Jawab

Sisi persegi alas $=\sqrt {256} = 16 $ cm
Tinggi segitiga TAB $=\sqrt {6^2 +8^2}=10 $ cm

Jadi Luas limas $\displaystyle = 4 \times TAB + ABCD = 4 \times \frac {1}{2}\times 16 \times 10 + 256 =320 + 256 = 576$ cm$^2$
Diketahui alas sebuah prisma berbentuk segitiga siku-siku dengan panjang sisi siku-sikunya 8 cm dan 6 cm. Jika tinggi prisma 18 cm, tentukan luas permukaan prisma.

Jawab

Luas $\bigtriangleup ABC = \frac{1}{2}\times 8 \times 6 = 24$ cm$^2$

Maka luas permukaan prisma tersebut

Luas $= 2 \times$ luas $\bigtriangleup ABC$ + Luas ACFD + Luas BCFE + Luas ABED

Luas $= 2 \times 24 + 6 \times 18 + 8 \times 18 + 10 \times 18 =48+108+144 + 180 = 480$ cm$^2$
Suatu kolam renang mempunyai ukuran panjang 40 m dan lebar 15 m. Kedalaman air pada ujung yang paling dangkal 1,3 m dan ujung yang paling dalam 2,7 m. Berapa liter volume air dalam kolam renang tersebut?

Jawab

Volume Kolam seluruhnya = luas trapesium $\times$ tinggi prisma

$\displaystyle = \frac{2,7+1,3}{2} \times 40 \times 15=1200$ m$^3=1.200.000$ liter
Suatu limas segi lima beraturan T.ABCDE tampak seperti gambar di bawah ini.

Panjang AB = 16 cm, OA = 10 cm, dan tinggi limas 20 cm. Hitunglah
a. luas alas limas;
b. volume limas.

jawab:

Tinggi $\bigtriangleup OAB = \sqrt{10^2-8^2}= \sqrt{36}=6$

a. luas alas limas $= 5\times \frac {1}{2}\times 16 \times 6= 240$ cm$^2$

b. Volume limas $\displaystyle = \frac{1}{3} \times$ luas alas $\times$ tinggi limas

$ \displaystyle = \frac {1}{3}\times 240 \times 20 =1600 $ cm$^3$

Jumat, 28 Januari 2022

Pembahasan tugas : Jari-jari lingkaran dalam dan luar segitiga

Latihan Soal:
Jari-Jari Lingkaran Dalam dan Luar Segitiga

dikumpulkan pada 29 Januari 2022

Kerjakan soal berikut dengan baik dan benar

Perhatikan gambar berikut ini.

Jika panjang AB = 8 cm, BC = 9 cm, dan AC $= \sqrt{145}$ cm, tentukan
a. luas ABC;
b. keliling ABC;
c. panjang jari-jari lingkaran dalam segitiga ABC.

Jawab:

a. Karena $\bigtriangleup ABC$ merupakan segitiga siku-siku maka berlaku

Luas $\displaystyle \bigtriangleup ABC= \frac{1}{2}\times BC \times AB = \frac{1}{2}\times 9 \times 8 = 36$ cm$^2$

b, Keliling $\bigtriangleup ABC = AB + BC + AC = 8 + 9 + \sqrt{145}=17 + \sqrt{145}$

c. panjang jari-jari lingkaran dalam $\bigtriangleup$

$\displaystyle r = \frac{\begin {matrix}luas & \bigtriangleup ABC \end {matrix}}{s}=\frac{36}{\frac{1}{2}\times \begin {matrix}keliling & \bigtriangleup ABC\end {matrix}}=\frac{36}{\frac {1}{2}\times(17+\sqrt{145})}=\frac{72}{17+\sqrt {145}}$
Perhatikan gambar berikut ini!

diketahui panjang AB = BC = AC = 9 cm. Tentukan
a. luas ' ABC;
b. panjang jari-jari lingkaran luar ' ABC.

Jawab

a. $\displaystyle s =\frac{1}{2}\times (AB+BC+AC) =\frac {1}{2}\times 3 \times 9 = \frac{27}{2}$ cm

luas $\displaystyle \bigtriangleup ABC =\sqrt{s(s-AB)(s-BC)(s-AC)}=\sqrt{ \frac{27}{2}\times ( \frac{27}{2}-9)^3}$

luas $\displaystyle \bigtriangleup ABC=\sqrt{ \frac{27}{2}\times \left ( \frac{9}{2} \right )^3}=\frac{27}{2}=\frac{81}{4}\sqrt 3$ cm$^2$

b. Panjang jari-jari lingkaran luar $\bigtriangleup ABC$

$\displaystyle r =\frac{AB\times BC\times AC}{4\times \begin {matrix} luas & \bigtriangleup ABC \end {matrix}}=\frac{3\times 9}{\frac {81}{4} \sqrt 3}=\frac{4}{3\sqrt 3}=\frac{4\sqrt 3}{9}$ cm
Panjang sisi miring suatu segitiga siku-siku adalah 26 cm dan panjang salah satu sisi siku-sikunya 10 cm. Tentukan
a. panjang jari-jari lingkaran dalam segitiga;
b. panjang jari-jari lingkaran luar segitiga.

Jawab

a = 10, c = 26 dan b = ? .Gunakan phytagoras untuk mencari b

$b=\sqrt {c^2-a^2}=\sqrt{26^2-10^2}=\sqrt{676-100}=\sqrt{576}=24$

Luas segitiga $\displaystyle =\frac{1}{2}\times a \times b = \frac{1}{2} \times 10 \times 24 = 120$ cm$^2$

$\displaystyle s = \frac{1}{2}(a + b + c)=\frac{1}{2}(10+24+26)=30$

a. $\displaystyle r =\frac {luas \bigtriangleup}{s}=\frac{120}{30}=4$ cm

b. $\displaystyle r =\frac{a\times b \times c}{4\times luas \bigtriangleup}=\frac{10\times 24\times 26}{4 \times 120}=13$ cm
Panjang sisi-sisi sebuah segitiga adalah 26 cm, 28 cm, dan 38 cm. Hitunglah
a. panjang jari-jari lingkaran dalam segitiga;
b. panjang jari-jari lingkaran luar segitiga.

Jawab:

$a=26, b=28$ dan $c=38$
$\displaystyle s=\frac{1}{2}(a+b+c)=\frac{1}{2}(26+28+38)=46$

luas $\bigtriangleup =\sqrt {s(s-a)(s-b)(s-c)}=\sqrt{46(46-26)(46-28)(46-38)}=\sqrt{46\times 20\times 18 \times 8}=24\sqrt {230} $ cm$^2$

a. panjang jari-jari lingkaran dalam segitiga =

$\displaystyle r =\frac {luas \bigtriangleup}{s}=\frac{24 \sqrt{230}}{46}=\frac{12 \sqrt 230}{23}$ cm

b. Panjang jari-jari lingkaran luar segitiga =

$\displaystyle r =\frac {a \times b \times c}{4\times luas \bigtriangleup}=\frac{26\times 28 \times 38}{4 \times 24 \sqrt{230}}=\frac{1729 \sqrt 230}{1380}$ cm
Panjang sisi-sisi sebuah segitiga adalah 8 cm, 15 cm, dan 17 cm. Hitunglah
a. panjang jari-jari lingkaran dalam segitiga;
b. panjang jari-jari lingkaran luar segitiga

jawab:

Jawab:

$a= 8, b=15$ dan $c=17$

$\displaystyle s=\frac{1}{2}(a+b+c)=\frac{1}{2}(8+15+17)=20$

luas $\bigtriangleup =\sqrt {s(s-a)(s-b)(s-c)}=\sqrt{20(20-8)(20-15)(20-17)}=\sqrt{20\times 12\times 5 \times 3}=60 $ cm$^2$

a. Panjang jari-jari lingkaran dalam segitiga =

$\displaystyle r =\frac {luas \bigtriangleup}{s}=\frac{60}{20}=3$ cm

b. Panjang jari-jari lingkaran luar segitiga =

$\displaystyle r =\frac {a \times b \times c}{4\times luas \bigtriangleup}=\frac{8\times 15 \times 17}{4 \times 60}=8,5$ cm

==== Selamat Mengerjakan ====

catatan:
Sebagai bahan acuan untuk mengerjakan soal tersebut, dapat kalian baca pada tautan berjudul "Menentukan panjang jari-jari lingkaran dalam dan luar segitiga"

Menentukan panjang sabuk lingkaran

Kalian tentu tahu rantai sepeda bukan? ya... rantai sepeda merupakan bagian dari sepeda yang digunakan sebagai penggerak sepeda. Nah, apakah kalian dapat menghitung panjang rantai sepeda jika diketahui panjang jari-jari gear sepeda? Pada pembahasan kali ini kita akan diperkenalkan contoh penyelesaian bagaimana menghitung panjang sabuk lingkaran. Dengan kalian mengetahui bagaimana langkah-langkah perhitungannya, kalian akan dapat menentukan sendiri panjang rantai sepeda.

Contoh 1

Dua buah gear sepeda memiliki jari-jari sama sebesar 14 cm. Tentukan panjang rantai yang menghubungkan gear speda tersebut!

jawab
perhatikan gambar berikut

Pada gambar di atas kita mengetahui bahwa dua gear memiliki jari-jari yang sama yakni 14 cm. Dengan demikian panjang $AB = CD = 2\times 14 = 28$ cm. Busur $\overset {\frown}{AD}=\overset {\frown}{BC}$. Kita akan menentukan panjang busur tersebut untuk mengetahui panjang rantai yang mengelilingi gear 1 dan gear 2.

Perhatikan bahwa busur $\overset AD$ merupakan $\frac{1}{2}$ keliling lingkaran. Karena busur Busur $\overset {\frown}{AD}=\overset {\frown}{BC}$ , Maka jelas bahwa jumlah panjang rantai yang mengelilingi gear 1 dan gear 2 tidak lain adalah keliling 1 buah gear itu sendiri. Sehingga kita dapatkan

panjang sabuk = keliling lingkaran $+ AB + CD \displaystyle = \pi \times diameter + 28 + 28 = \frac {22}{7} \times 28 + 56 = 88 + 56 = 144$ cm

Jadi panjang rantai yang dibutuhkan adalah 144 cm

Contoh 2

Diketahui 3 buah lingkaran memiliki jari-jari 7 cm diikat sedemikian rupa seperti gambar berikut ini:

Hitunglah panjang tali yang dibutuhkan untuk mengikat ke tiga lingkaran tersebut!

Jawab:
perhatikan gambar berikut ini

Ketiga lingkaran masing-masing memiliki titik pusat di A, B dan C. Karena masing-masing lingkaran memiliki jari-jari 7 cm, maka panjang AB = BC = AC = 7 +7 =14 cm. $\bigtriangleup ABC$ merupakan segitiga sama sisi, sehingga $\angle ABC = \angle BCA = \angle BAC = 60^o$. Selain itu karena letaknya yang kosentris terhadap segitiga sama sisi ABC, maka panjang busur $\overset{\frown}{DI}=\overset{\frown}{UF}=\overset{\frown}{GH}$, Kita akan menentukan panjang masing busur ini untuk menentukan panjang tali yang melingkari masing-masing lingkaran.

Perhatikan lingkaran yang berpusat di A
karena ABDE, BCGF dan ACHI adalah persegi panjang maka $\angle DAB = \angle IAC=90^2$ dan = AB = 14
Dengan demikian kita dapat menentukan besar sudut $\angle DAI$ yakni
$\angle DAI =360^o - \angle DAB - \angle IAC - \angle BAC=360^o-90^o-90^o-60^o=120^o$

Berdasarkan teori garis singgung lingkaran, maka kita dapatkan

Panjang busur $\displaystyle \overset{\frown}{DI}= \frac{\angle DAI}{360^o}\times \begin {matrix} keliling&lingkaran&A \end {matrix}=\frac {120^o}{360^o}\times \frac {22}{7}\times 14=\frac {1}{3}\times 44=\frac {44}{3}$ cm

Dengan demikian panjang sabuk ketiga lingkaran tersebut dapat kita cari, yakni

Panjang sabuk $=\overset{\frown}{DI}+\overset{\frown}{UF}+\overset{\frown}{GH}+ DE + FG + HI$
$\Leftrightarrow$ $\displaystyle = 3 \times (\overset{\frown}{DI} + AB) = 3 \times (\frac {44}{3}+14)=44 +42=86$ cm

Jadi panjang tali yang dibutuhkan $\geq$ dari 86 cm.

Contoh 3

Gambar di atas adalah penampang enam buah drum yang berbentuk tabung dengan jari-jari 24 cm. Hitunglah panjang tali minimal yang diperlukan untuk mengikat enam buah drum tersebut.

Jawab:
sama seperti pada contoh 2, keenam lingkaran tersebut tersusun secara konsentris terhadap segitiga sama sisi yang panjang sisinya $= 4 \times 24 = 96$ cm. Karena kedudukannya yang konsentris maka besar sudut yang terbentuk pada busur yang dikeliling tali (lingkaran 1, 4 dan 6) sebesar $120^o$. Dengan demikian

panjang busur $=3 \times$ panjang sisi segitiga sama sisi + $3 \times$ panjang busur yang dikeliling tali $ =3 \times 96 + 3 \times \frac {120^o}{360^o}\times 3,14 \times 48 =288 +150,72= 438,72$ cm

==== Selamat Belajar ====

Kamis, 27 Januari 2022

Pembahasan Tugas harian 1: garis singgung lingkaran kelas 8 SMP (27 Januari 2022)

Latihan Soal Garis Singgung Lingkaran
Kelas 8 SMP
Tugas dikumpulkan pada 27 Januari 2022
dikirim langsung melalui alamat email: altissimastudycenter@gmail.com

Kerjakan soal berikut dengan benar

Dari garis-garis k, l, m, n, dan p pada gambar di atas, manakah yang merupakan garis singgung lingkaran?

jawab:

Salah satu ciri khas garis singgung lingkaran adalah tidak memotong lingkaran di dua titik tetapi menyentuh lingkaran di satu titik. Oleh karena itu garis yang menyinggung lingkaran pada gambar tersebut adalah garis l, garis n dan garis j.
Lukislah pada kertas berpetak lingkaran berpusat di titik O(0, 0) dengan jari-jari 5 satuan panjang. Selanjutnya lukislah garis singgung lingkaran yang melalui titik A(0, 5).

jawab
Lukislah pada kertas berpetak lingkaran dengan pusat di titik P(3, 2) dan jari-jari 4 satuan panjang. Selanjutnya, lukislah garis singgung lingkaran yang melalui titik Q(–1, 2).

jawab :
Berdasarkan keterangan pada gambar berikut, hitunglah panjang setiap garis singgung lingkarannya.

jawab

(i) $AB=\sqrt{OB^2-OA^2}=\sqrt{7^2-5^2}=\sqrt{49-25}=\sqrt{24}=2\sqrt 6$ cm

(ii) $PQ=\sqrt{OP^2-OQ^2}=\sqrt{20^2-12^2}=\sqrt{400-144}=\sqrt{256}=16$ cm

(iii) $XY=\sqrt{OX^2-OY^2}=\sqrt{26^2-10^2}=\sqrt{676-100}=\sqrt{576}=24$ cm
Perhatikan gambar berikut:

Garis AB dan BC adalah garis singgung lingkaran yang melalui titik A. Jika OA = 10 cm dan OB = 26 cm maka tentukan
a. panjang garis singgung AB;
b. luas layang-layang OBAC;
c. panjang tali busur AC.
jawab

a. $AB=\sqrt{OB^2-OA^2}=\sqrt{26^2-10^2}=\sqrt{676-100}=\sqrt{576}=24$ cm

b. Luas $\displaystyle \bigtriangleup OAB=\frac{1}{2} \times AB \times OA= \frac{1}{2}\times 24 \times 10 = 120$ cm$^2$

Jadi luas layang-layang $= 2\times \bigtriangleup OAB = 2 \times 120=240$ cm$^2$

c. Misalkan D adalah titik potong diagonal layang-layang
Dengan menggunakan perbandingan luas kita dapatkan

Luas $\displaystyle \bigtriangleup OAB=\frac{1}{2} \times OB \times AD$

$\displaystyle 120 =\frac{1}{2} \times 26 \times AD$

$\displaystyle AD =\frac{120}{13} $

dengan demikian panjang tali busur layang $\displaystyle AC = 2 \times AD = 2 \times \frac {120}{13} = \frac {240}{13}$ cm
Perhatikan gambar berikut.

Berdasarkan gambar tersebut, benar atau salahkah pernyataan-pernyataan berikut?
a. AB sejajar PQ
b. AP tegak lurus PQ
c. AB = CD
d. AB = PQ
e. AP tegak lurus AB di titik A

jawab:
a. salah karena $\angle PAB \neq \angle APQ$ dan $\angle ABQ \neq \angle PQB$
b. Benar berdasarkan sifat garis singgung lingkaran.
c. Benar berdasarkan sifat garis singgung persekutuan luar lingkaran
d. Salah karena AB adalah ruas garis singgung persekutuan luar lingkaran, sedangkan PQ jarak titik pusat kedua lingkaran. berdasarkan sifat garis singgung persekutuan luar panjang PQ > panjang AB
Panjang jari-jari dua lingkaran masing-masing adalah 12 cm dan 5 cm. Jarak kedua titik pusatnya adalah 24 cm. Hitunglah
a. panjang garis singgung persekutuan dalam;
b. panjang garis singgung persekutuan luarnya.

Jawab
diketahui p = 24, R = 12 dan r = 5
a. $d = \sqrt{p^2-(R+r)^2}=\sqrt{24^2-(12+5)^2}=\sqrt{576 - 289}=\sqrt {287}$ cm

b. $d =\sqrt{p^2-(R-r)^2}=\sqrt{24^2-(12-5)^2}=\sqrt{576 - 49}=\sqrt {527}$ cm
Perhatikan gambar di atas.

Panjang jari-jari lingkaran yang berpusat di O adalah 9 cm dan panjang jari-jari lingkaran yang berpusat di P adalah 4 cm. Jika panjang garis singgung persekutuan luarnya 12 cm, tentukan
a. jarak kedua pusat lingkaran;
b. luas segi empat yang diarsir

Jawab

Diketahui d = 12 cm, R = 9 cm dan r = 4 cm

a. $p = \sqrt {d^2+(R-r)^2}=\sqrt{12^2+(9-4)^2}=\sqrt{144 + 25}=\sqrt {13}$ cm
b. Luas daerah yang diarsir $=2 \times \begin {matrix} luas & trapesium \end {matrix}= 2\times \frac{1}{2}\times (R+r) \times AB=2 \times \frac{1}{2} \times (9+4)\times 12 =156$ cm$^2$
Panjang garis singgung persekutuan dalam dua lingkaran adalah 24 cm dan jarak kedua pusatnya adalah 26 cm. Jika panjang salah satu jari-jari lingkaran 6 cm, hitunglah panjang jari-jari lingkaran yang lain.

Jawab
diketahui d = 24 cm, p =26 cm dan R = 6 cm
$R + r = \sqrt{p^2 - d^2}$
$ 6 + t = \sqrt{26^2-6^2}=\sqrt{676-576}=\sqrt{100}=10$ $\Leftrightarrow$ $r =10-6=4 cm$
Panjang jari-jari dua buah lingkaran yang berpusat di O dan P masing-masing adalah 8 cm dan 4 cm. Jarak kedua titik pusatnya 20 cm.
a. Lukislah garis singgung persekutuan dalamnya.
b. Hitunglah panjang garis singgung persekutuan dalam tersebut.

Jawab
diketahui R = 8 cm, r = 4 cm dan p = 20 cm

a,

b. $d = \sqrt{p^2-(R+r)^2}=\sqrt{20^2-(8+4)^2}=\sqrt{400 - 144}=\sqrt {256}=16$ cm

Bahan acuan untuk mengerjakan soal ini:

Senin, 24 Januari 2022

Beberapa Teorema Sudut Pusat dan Sudut Keliling pada Lingkaran

Sudut Pusat dan Sudut Keliling pada Lingkaran

Beberapa waktu lalu kalian sudah mengenal apa itu sudut pusat dan sudut keliling. Sebagaimana kalian ketahui, sudut pusat adalah sudut yang dibentuk dari dua buah jari-jari yang berpotongan di titik pusat lungkaran. Sementara, sudut keliling adalah sudut yang dibentuk dari tali busur yang berpotongan di titik yang terdapat pada keliling lingkaran. Hubungan sudut pusat dan sudut keliling adalah

Sudut pusat $=2 \times$ sudut keliling

Pada pembahasan berikut, kita akan membahas lebih jauh hal-hal yang berkaitan dengan sudut pusat dan sudut keliling. Beberapa diantaranya adalah menentukan besarnya sudut keliling yang menghadap diameter lingkaran, menentukan besarnya sudut keliling yang menghadap busur linkaran yang sama, dan menentukan besarnya sudut pada segiempat tali busur. Kita akan membahasnya satu persatu.

A. Sudut Pusat besarnya 2 kali sudut keliling

Pada awal pertemuan kita sudah diperkenalkan sebuah pernyataan bahwa besarnya sudut pusat sama dengan dua kali besarnya sudut keliling. Tentu saja pernyataan ini dapat dibuktikan kebenarannya bila kita memperhatikan penjelasan berikut ini:

Perhatikan gambar

Pada gambar tersebut, $\angle BAC$ merupakan sudut keliling dan $\angle BOC$ merupakan sudut pusat. Kedua sudut ini menghadap busur yang sama yakni busur $\overset {\frown} {BC}$. Sekarang, apabila kita menarik garis lurus melalui titik A dan titik pusat lingkaran maka kita akan dapatkan gambar sebagai berikut:

Perhatikan bahwa bila $\angle OAB = x$ dan $\angle OAC = y$ maka dengan memperhatikan $\bigtriangleup AOB$ dan $\bigtriangleup AOC$ kita dapatkan

$\angle BOC =\angle BOD +\angle COD$ ...... persamaan 1

$\angle BAC =\angle OAB +\angle OAC = x+y $ ...... persamaan 2

Padahal kita tahu panjang $\overline {OA}=\overline OB =\overline OC= r $. Dengan demikian $\bigtriangleup AOB$ dan $\bigtriangleup AOC$ merupakan segitiga sama kaki. Akibatnya $\angle OAB = \angle OBA$ dan $\angle OAC =\angle OCA$.

Pada $\bigtriangleup AOB$ $\Leftrightarrow$ $\angle AOB=180^o-(\angle OAB + \angle OBA) =180^o-(x+x)=180^o-2x$ ..... persamaan 3

Pada $\bigtriangleup AOC$ $\Leftrightarrow$ $\angle AOC=180^o-(\angle OAC + \angle OCA) =180^o-(y+y)=180^o-2y$ ..... persamaan 4

Tetapi kita tahu bahwa $\angle BOD$ merupakan pelururs dari $\angle AOB$ dan $\angle COD$ merupakan pelururs dari $\angle AOC$. dengan demikian jika kita memperhatikan persamaan 3 dan persamaan 4 maka kita dapatkan

$\angle BOD = 180^o - \angle AOB =180^o-(180^o-2x)=2x$

$\angle COD = 180^o - \angle AOC =180^o-(180^o-2y)=2x$

Dari dua persamaan terakhir dan dengan melihat persamaan 1 dan persamaan 2 kita dapatkan

$\angle BOC =\angle BOD +\angle COD=2x+2y = 2 (x+y) = 2 \times \angle BAC $

Dengan demikian terbukti bahwa besarnya sudut pusat sama dengan $2\times$ sudut keliling.

B. Hubungan sudut pusat dengan keliling dan luas lingkaran

Perhatikan gambar berikut:

Karena juring AOB merupakan bagian dari lingkaran yang berpusat di O, maka berlaku hubungan perbandingan, yakni

$\displaystyle \frac {\angle AOB}{360^o}=\frac{\begin {matrix} busur & \overset{\frown}{AB}\end {matrix}}{\begin {matrix} keliling & lingkaran \end {matrix}}=\frac {\begin {matrix} luas & juring & AOB \end {matrix}}{\begin {matrix} luas & lingkaran \end {matrix}}$

C. Besarnya sudut keliling yang menghadap diameter

Perhatikan gambar berikut ini

Pada gambar tersebut nampak bahwa $\angle ACB$ merupakan sudut keliling yang menghadap diameter $\overline {AB}$. Sebagaimana kita tahu bahwa sudut satu putaran penuh = $360^o$ dan diameter lingkaran membagi dua lingkaran sama besar. Dengan demikian besarnya $\angle AOB = 180^o$. Kita pun tahu bahwa $\angle AOB$ dan $\angle ACB$ menghadap busur yang sama sehingga mereka mempunyai hubungan sebagai sudut pusat dan sudut keliling. Dengan demikian karena sudut pusat $=2\times$ sudut keliling maka diperoleh:

$\displaystyle \angle ACB =\frac{1}{2}\times \angle AOB=\frac{1}{2}\times 180^o=90^o$

Nah, dengan demikian kita dapat menyimpulkan bahwa

Semua sudut keliling yang menghadap diameter lingkaran memiliki sudut sebesar $90^o$
Semua sudut keliling yang menghadap diameter lingkaran memiliki 2 tali busur yang saling tegak lurus.

Semua sudut keliling yang menghadap
diameter lingkaran memiliki sudut sebesar $90^o$

D. Sudut keliling yang menghadap busur yang sama

Untuk melihat hubungan antara sudut keliling yang menghadap busur yang sama, kalian bisa memperhatikan gambar berikut ini:

Perhatikan bahwa $\angle DOE$ merupakan sudut pusat dan $\angle DAE, \angle DBE$ dan $\angle DCE$ merupakan sudut keliling yang menghadap busur yang sama yakni busur $\overset {\frown}{DE}$. Karena kita tahu bahwa hubungan antara sudut pusat dan sudut keliling yang menghadap busur yang sama adalah sudut pusat = $2\times$ sudut keliling maka :

$\displaystyle \angle DAE = \frac{1}{2} \times \angle DOE$

$\displaystyle \angle DBE = \frac{1}{2} \times \angle DOE$

$\displaystyle \angle DCE = \frac{1}{2} \times \angle DOE$

sehingga kita dapatkan

$\angle DAE = \angle DBE=\angle DCE$

Dengan demikian kita dapat menyimpulkan bahwa

Semua sudut keliling yang menghadap pada busur yang sama seperti halnya dengan sudut pusat, maka besarnya semua sudut keliling tersebut sama yakni setengah dari sudut pusatnya.

==== Selamat Belajar ====

Sabtu, 15 Januari 2022

Join together with Altissima Study Center
By
Subscribe and like this channel,

give positive comment

support our efforts and hard work,

If you want to contact us, please send your email at altissimastudycenter@gmail.com