Cara Menentukan Limit Fungsi
Pada pertemuan sebelumnya, kalian sudah mengetahui bahwa $\displaystyle \lim_{x \rightarrow 2} \frac{x^2-4}{x-2} =4$ melalui pendekatan intuitif, yakni dengan menggunakan daftar tabel dan grafik fungsinya. Meskipun metode seperti ini dapat digunakan untuk menentukan nilai limitnya, namun upaya menentukan nilai tersebut membutuhkan waktu yang cukup lama. Pertanyaan selanjutnya adalah, adakah teknik khusus dalam menentukan nilai limit fungsi tanpa harus menggunakan daftar tabel beserta grafiknya? Jawaban atas pertanyaan tersebut tentu ada. Pada pembahasan kali ini kita akan mempelajari materi tentang bagaimana menentukan nilai limit fungsinya. Beberapa metode tersebut diantaranya adalah metode subtitusi, pemfaktoran dan perkalian sekawan.
A. Metode Subtitusi
Ketika kalian berhadapan dengan limit fungsi, langkah pertama yang wajib kalian usahakan adalah mensubtitusikan nilai $x=c$ untuk mencari nilai $\displaystyle \lim_{x \rightarrow c}f(x)$. Jika hasil yang didapat nilainya ada (misalnya $f(c)=L$) dan bukan berbentuk $\displaystyle f(c)=\frac {0}{0}$,
Contoh 1
Tentukan nilai dari $\displaystyle \lim_{x \rightarrow 3} \frac{x^2-4}{x-2}$
Jawab
jika kita subtitusikan $x=3$ ke dalam fungsi $f(x)$ maka kita dapatkan
$\displaystyle f(3) =\frac {3^2-4}{3-2}=\frac{9-4}{1}=5$
Dengan demikian
$\displaystyle \lim_{x\rightarrow 2}\frac{x^2-4}{x-2}= 5$
Lalu bagaimana jika $f(c) =\frac {0}{0}$. Tentu saja metode subtitusi tidak dapat digunakan karena kita melakukan pendekatan terhadap nilai $f(x)$ ketika x mendekati c. Kita akan menggunakan metode lainnya dalam menentukan nilai limit $f(x)$. Namun sebelum melangkah lebih jauh, ada hal penting yang perlu kalian perhatikan yakni, di dalam beberapa kasus kita bisa menduga ada faktor dari $f(x)$ yang menyebabkan ketika $x=c$, maka nilai $\displaystyle f(c) =\frac{0}{0}$. Dugaan sementara tentu saja faktor tersebut adalah $(x-c)$.
Pada kasus $\displaystyle \frac{x^2-4}{x-2}$ misalnya, kita dapat menduga bahwa ketika $x=2$, maka faktor yang menyebabkan nilai $\displaystyle f(2) =\frac {0}{0}$ adalah $(x-2)$. Jika memang demikian, maka kita akan mengeliminasi faktor $(x-2)$ ini sehingga menghasilkan fungsi $\displaystyle f(x) =\frac{x^2-4}{x-2}$ seolah-olah menjadi bentuk fungsi yang lebih sederhana. Beberapa diantaranya adalah metode pemfaktoran dan perkalian sekawan.
B. Metode Pemfaktoran
$\displaystyle f(x) =\frac{x^2-4}{x-2}$
$\Leftrightarrow$ $\displaystyle f(x) =\frac{(x-2)(x+2)}{x-2}$
$\displaystyle \lim_{x \rightarrow 2}\frac{x^2-4}{x-2}=x+2=2+2=4$
Contoh 2
Tentukan nilai dari $\displaystyle \lim_{x\rightarrow 3} \frac {x^2-5x+6}{2x^2-5x-3}$
Jawab :
Kita akan cek terlebih dahulu nilai $\displaystyle f(x) =\frac{x^2-5x+6}{2x^2-5x-3}$ untuk $x = 3$, yakni:
$\displaystyle f(3)=\frac{3^2-5.3+6}{2.3^2-5.3-3}=\frac{9-15+6}{18-15-3}=\frac{0}{0}$
Dengan demikian kita harus menggunakan cara lain, yakni pemfaktoran.
$\displaystyle \lim_{x \rightarrow 3} \frac {x^2-5x+6}{2x^2-5x-3}=\lim_{x \rightarrow 3} \frac{(x-2)(x-3)}{(2x+1)(x-3)}$
$\Leftrightarrow$ $\displaystyle =\frac{x-2}{2x+1}=\frac{3-2}{2.3+1}=\frac{1}{7}$
C. Perkalian Sekawan
$\displaystyle 1 = \frac{3}{3}=\frac {a+b}{a+b}=\frac {\sqrt{a-b}}{\sqrt{a-b}}=\frac{\sqrt a -\sqrt b}{\sqrt a -\sqrt b}=...$ dst
Beberapa contoh kawan dari suatu fungsi adalah sebagai berikut:
- $p(x) = a + b$ maka kawanya adalah $\displaystyle \frac {a - b}{a-b}$
- $p(x) = \sqrt {a - b}$ maka kawanya adalah $\displaystyle \frac {\sqrt{a + b}}{\sqrt{a-b}}$
- $p(x) = \sqrt {a + b}-\sqrt{a-b}$ maka kawanya adalah $\displaystyle \frac {\sqrt {a +b}+\sqrt{a-b}}{\sqrt{a+b}+\sqrt {a-b}}$
Contoh 3
Tentukan nilai dari $\displaystyle \lim_{x \rightarrow 3} \frac {3-\sqrt{18-x^2}}{x-3}$
jawab
Ketika nilai $x = 3$ kita subtitusikan ke dalam fungsi $f(x)$ maka kita dapatkan:
$\displaystyle f(3)= \frac {3-\sqrt{18-3^2}}{3-3}=\frac {3-\sqrt 9}{0} =\frac {0}{0}$
karena itu kita tidak dapat menggunakan metode subtitusi. Akan kita coba dengan menggunakan metode perkalian sekawan, yakni:
$\displaystyle \lim_{x \rightarrow 3} \frac {3-\sqrt{18-x^2}}{x-3}=\lim_{x \rightarrow 3}\frac{3-\sqrt {18-x^2}}{x-3}\times \frac {3+\sqrt {18x^2}}{3+\sqrt {18-x^2}}$
$\Leftrightarrow$ $\displaystyle =\lim_{x \rightarrow 3}\frac {9-(18-x^2)}{(x-3) \left ( 3+\sqrt {18-x^2}\right )}$
Dengan demikian kita sudah diperkenalkan 3 macam teknik dasar dalam menentukan nilai dari limit fungsi. Sebenarnya masih ada 1 teknik lagi yang juga cukup ampuh yakni D'hospital. Namun teknik ini memerlukan pemahaman lebih lanjut yakni turunan yang nanti juga akan kalian pelajari setelah kalian menguasai materi limit fungsi. Pada kesempatan kali ini saya hanya akan menunjukan sedikit teorema D'Hospital yang berhubungan dengan limit fungsi:
Teorema D'Hospital :


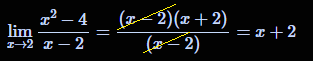
Tidak ada komentar:
Posting Komentar