Contoh soal Hots tentang Persamaan garis singgung persekutuan lingkaran

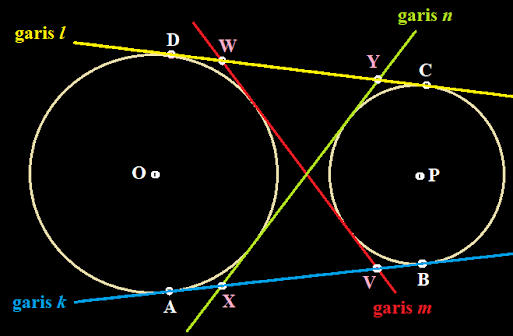
1. Lingkaran I dan lingkaran II masing-masing titik pusatnya terletak di titik O dan titik P. Kedua lingkaran tersebut berada dalam kedudukan terpisah satu dengan yang lainnya.  Garis k dan garis l adalah garis singgung persekutuan luar kedua lingkaran tersebut. Garis k menyinggung lingkaran I di titik A dan menyinggung lingkaran II di titik B. Garis l menyinggung lingkaran I di titik D dan menyinggung lingkaran II di titik C. Selain itu garis m dan garis n adalah garis singgung persekutuan dalam kedua lingkaran tersebut. Garis m memotong garis k dan garis l masing-masing di titik V dan di titik W. Garis n memotong garis k dan l di titik X dan di titik Y.
   
   Tunjukan bahwa AB = CD = VW = XY
   
   
   

   
   
   
   
   jawab:         
   
   perhatikan gambar berikut ini:|
   
   
   
   
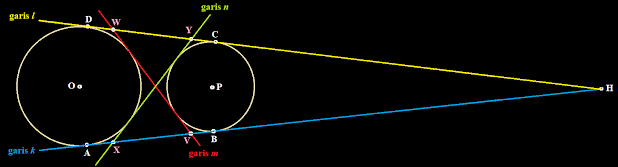
   Jika kita membuat perpanjangan garis k dan garis l sedemikian sehingga berpotongan pada titik H, maka akan kita dapatkan
                                                         AB = AH - BH
                                                         CD = DH - CH
   
   Tetapi berdasarkan sifat garis singgung lingkaran yang berpotongan di luar lingkaran didapat
                                                         AH = DH
                                                         BH = CH
   Akibatnya
                                                      AB = AH - BH
                                                      AB = DH - CH = CD ..... persamaan 1
   
   Kemudian, misalkan titik Q, R, S, dan T masing-masing merupakan titik singgung garis persekutuan dalam lingkaran dan U adalah titik potong garis singgung persekutuan dalam tersebut seperti pada gambar berikut ini:
   
   
   

   
   

   
   
   Nampak pada gambar  bahwa 
                CD = CY + YD
                QY = YS +  QS
   
   Tetapi berdasarkan sifat dua garis singgung yang berpotongan di luar lingkaran kita tahu bahwa :
                CY  = YS
                YD = QY
   
   Oleh karena itu 
                 CD = CY + YD = YS + QY = YS + (YS + SQ) = 2 YS + QS ...... persamaan 2
   
   Selain itu pada gambar nampak:
                 AB = AX + XB
                 XS = XQ + QS
   
   berdasarkan sifat dua garis singgung yang berpotongan di luar lingkaran kita tahu bahwa :
                 XS = XB
                 AX = XQ
   
   Oleh karena itu didapat :
                AB = AX + XB = XQ + XS = XQ + (XQ + QS) = 2 XQ + QS ,,,,,,,, persamaan 3
   
   Karena AB = CD maka dari persamaan 2 dan persamaan 3 diperoleh
               AB = CD
   2 YS + QS = 2 XQ + QS
          YS      =        XQ   ........ persamaan 4
   
   dari persamaan 1, persamaan 2 dan persamaan 4 
   
                       AB = CD = YD + CY = QY + YS = YQ + XQ = XY
   
   Dengan demikian telah ditunjukan bahwa AB = CD = XY.
   
   Sekarang, dengan analogi yang sama kita juga dapat menunjukan bahwa AB = CD = VW, yakni 
   
   Nampak pada gambar  bahwa 
                CD = WD + CW
                RW = WT +  TR
   Tetapi berdasarkan sifat dua garis singgung yang berpotongan di luar lingkaran kita tahu bahwa :
                WD  = WT
                RW  = CW
   
   Oleh karena itu 
                 CD = WD + CW = WT + RW = WT + (WT + TR) = 2 WT + TR ...... persamaan 5
   
   Selain itu pada gambar nampak:
                 AB = AV + VB
                 VT = VR + TR
   
   berdasarkan sifat dua garis singgung yang berpotongan di luar lingkaran kita tahu bahwa :
                 VT = AV
                 VB = VR
   
   Oleh karena itu didapat :
                AB = AV + VB = VT + VR = (VR +TR)+ VR = 2 VR + TR ,,,,,,,, persamaan 6
   
   Karena AB = CD maka dari persamaan 5 dan persamaan 6 diperoleh
               AB = CD
   2 VR + TR = 2 WT + TR
          VR      =        WT   ........ persamaan 7
   
   dari persamaan 1, persamaan 5 dan persamaan 7 
   
                       AB = CD = WD + CY = WT + RW = VR + RW = VW
   
   Dengan demikian telah ditunjukan bahwa AB = CD = VW
   
   Karena AB = CD = XY dan AB = CD = VW maka berlaku AB = CD = VW = XY
   

==== Good Luck ====