Menentukan Panjang Jari - Jari Lingkaran Dalam dan Luar Segitiga
Setelah kita membahas materi tentang
sabuk pada lingkaran, kali ini kita akan mempelajari materi mengenai bagaimana menentukan panjang jari-jari lingkaran dimana tiga titik pada lingkaran tersebut masing-masing menyinggung sisi-sisi pada segitiga. Pada pembahasan kali ini. kita akan mengenal istilah jari-jari lingkaran dalam segitiga dan jari-jari lingkaran luar segitiga. Namun sebelum kita mengenal lebih jauh mengenai hal itu, kita akan diperkenalkan terlebih dahulu teknik menghitung luas segitiga bila diketahui panjang ketiga sisinya.
A. Menentukan Luas Segitiga Bila Diketahui Panjang Sisi-Sisinya.
Perhatikan gambar berikut ini:
Gambar di atas menunjukan bahwa segitiga $\bigtriangleup ABC$ memiliki panjang sisi AB =
c, AC =
b dan BC =
a. Jika kita menarik garis tegak lurus BC dan melalui A, maka akan didapatkan titik potong garis tegak lurus tersebut dengan garis BC. Misalkan saja titik potong tersebut adalah D. Apabila kita andaikan panjang BD = x, maka panjang CD =
a - x. Dengan demikian berdasarkan rumus Phtagoras kita dapatkan:
$t^2 = c^2 - x ^2$ dan $t^2 = b^2 - (a-x)^2$ ........ persamaan 1
jika kita subtitusikan kedua persaman tersebut maka kita akan mendapatkan
$c^2 - x ^2 = b^2 - (a-x)^2$
$c^2 - x ^2 = b^2 - a^2+2ax- x^2$
$c^2 - b ^2 + a^2= 2ax$
$\displaystyle x = \frac {c^2 - b ^2 + a^2}{2a}$
kita subtitusikan persamaan terakhir ke dalam bagian pertama persamaan 1 didapat
$t^2 = c^2 - x ^2$
$\displaystyle t^2 = c^2 - \left ( \frac{c^2-b^2+a^2}{2a} \right) ^2$ ingat $p^2 - q^2 = (p-q) (p+q)$
$\displaystyle t^2 = \left ( c+\frac{c^2-b^2+a^2}{2a} \right) \left ( c-\frac{c^2-b^2+a^2}{2a} \right )$
$\displaystyle t^2 = \left (\frac{2ac+c^2-b^2+a^2}{2a} \right) \left ( \frac{2ac-(c^2-b^2+a^2)}{2a} \right )$
$\displaystyle t^2 = \left (\frac{c^2-b^2+a^2+2ac}{2a} \right) \left ( \frac{-c^2+b^2-a^2+2ac}{2a} \right )$
$\displaystyle t^2 = \left (\frac{c^2+2ac+a^2-b^2}{2a} \right) \left ( \frac{b^2-(c^2-2ac+a^2)}{2a} \right )$
$\displaystyle t^2 = \left (\frac{(c+a)^2-b^2}{2a} \right) \left ( \frac{b^2-(c-a)^2}{2a} \right )$
$\displaystyle t^2 = \left (\frac{(c+a+b)(c+a-b)}{2a} \right) \left ( \frac{(b+c-a)(b-(c-a))}{2a} \right )$
$\displaystyle t^2 = \left (\frac{(c+a+b)(c+a-b)}{2a} \right) \left ( \frac{(b+c-a)(b-c+a))}{2a} \right )$ ..... persamaan 2
Sekarang misalkan $\displaystyle s =\frac {1}{2}\times keliling$ $\displaystyle \bigtriangleup ABC=\frac{1}{2}(a+b+c)$, maka
$a+b+c =2s$ $c+a = 2s - b$ $a+b = 2s - c$ $b+c=2s -a$ ..... persamaan 3
Sehingga dari persamaan 2 dan persamaan 3 diperoleh
$\displaystyle t^2 = \left (\frac{(c+a+b)(c+a-b)}{2a} \right) \left ( \frac{(b+c-a)(b-c+a))}{2a} \right )$
$\displaystyle t^2 = \left (\frac{(s)((2s-b)-b)}{2a} \right) \left ( \frac{((2s-a)-a)((2s-c)-c)}{2a} \right )$
$\displaystyle t^2 = \left (\frac{(2s)(2s-2b)}{2a} \right) \left ( \frac{(2s-2a)(2s-2c)}{2a} \right )$
$\displaystyle t^2 = \left (\frac{2(2s)(s-b)}{2a} \right) \left ( \frac{2(s-a) 2(s-c)}{2a} \right )$
$\displaystyle t^2 = \left (\frac{4(s)(s-b)(s-b)(s-a)}{a^2} \right) $
$\displaystyle t = \frac{2}{a}\sqrt{(s)(s-b)(s-b)(s-a) } $
Karena Luas $\bigtriangleup ABC = \frac {1}{2}\times a \times t$, maka dari persamaan terakhir diperoleh
Luas $\displaystyle \bigtriangleup ABC = \frac {1}{2}\times a \times \frac{2}{a}\sqrt{(s)(s-b)(s-b)(s-a) }$
Luas $\bigtriangleup ABC = \sqrt{(s)(s-b)(s-b)(s-a) }$
Dengan demikian kita sudah dapat menyimpulkan bahwa
Rumus :
" Jika sebuah segitiga memiliki panjang sisi masing-masing adalah a, b dan c, maka luas segitiga tersebut adalah
Luas $=\sqrt {s (s-a)(s-b)(s-c)}$ dimana $\displaystyle s = \frac{1}{2}\times (a+b+c)$
B. Jari-jari Lingkaran Dalam Segitiga
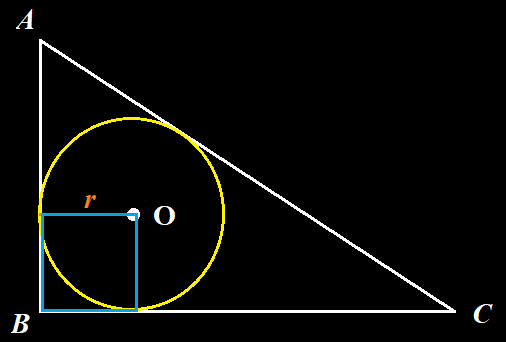
Sekarang perhatikan gambar berikut ini
Pada gambar di atas nampak a, b, dan c adalah panjang sisi masing-masing segitiga. Setiap sisi segitiga tersebut bersinggungan dengan sebuah lingkaran yang terdapat pada segitiga tersebut. Kita akan menunjukan hubungan antara luas segitiga, panjang sisi segitiga dan jari-jari lingkaran dalam segitiga tersebut.
Perhatikan bahwa segitiga $\bigtriangleup ABC$ terbagi dalam 3 buah segitiga yakni : $\bigtriangleup AOB. \bigtriangleup AOC$ dan $\bigtriangleup BOC$. Jari-jari lingkaran yang terdapat di dalam $\bigtriangleup ABC$ merupakan tinggi dari setiap segitiga tersebut. Dengan demikian
Luas $\bigtriangleup ABC =$ luas $\bigtriangleup AOB$ + luas $\bigtriangleup AOC$ + luas $\bigtriangleup BOC$
Luas $\displaystyle \bigtriangleup ABC =\frac {1}{2}. c . r + \frac {1}{2}.b.r + \frac{1}{2}.a.r$
Luas $\displaystyle \bigtriangleup ABC =\frac {1}{2} r . (a+b + c)$
karena (a+b+c) = 2s dan luas segitiga $=\sqrt {s(s-a)(s-b)(s-c)}$ maka kita dapatkan
Luas $\displaystyle \bigtriangleup ABC =\frac {1}{2} r . (a+b + c)$
Luas $\displaystyle \bigtriangleup ABC =\frac {1}{2} r . 2s$
$\displaystyle r= \frac {\begin {matrix} luas&\bigtriangleup ABC \end {matrix}}{s}=\frac{\sqrt {s(s-a)(s-b)(s-c)}}{s}$
Dengan demikian kita dapat menyimpulkan bahwa
"Panjang jari-jari lingkaran dalam segitiga sama dengan luas segitiga dibagi setengah dari keliling segitiga, yakni:
$\displaystyle r= \frac {\begin {matrix} luas&\bigtriangleup ABC \end {matrix}}{s}=\frac{\sqrt {s(s-a)(s-b)(s-c)}}{s}$
C. Jari-jari Lingkaran Luar Segitiga
Untuk memahami jari-jari lingkaran luar segitiga, kalian bisa mengamti gambar berikut ini:
Gambar di atas menunjukan bahwa sebuah segitiga $\bigtriangleup ABC$ berada di dalam lingkaran yang berjari-jari. Setiap sudut dari $\bigtriangleup ABC$ menyinggung lingkaran yang berpusat di O. Panjang sisi $AB =c , BC = a$ dan $AC = b$. Kita akan menentukan apakah ada hubungan antara jari-jari lingkaran dengan panjang ketiga sisi segitiga tersebut. Sebagai gambaran awalny, coba kalian membuat garis AD yang tegak lurus dengan garis BC. Kemudian kalian buat perpanjangan garis AO sampai memotong lingkaran di titik E. Maka kalian akan mendapati gambar seperti berikut ini:
Kalau kalian amati, AE merupakan diameter lingkaran dan $\angle ACE$ merupakan sudut keliling yang menghadap busur $\overset{\frown}{AE}$. Berdasarkan sifat sudut keliling dan sudut pusat, maka kita dapatkan:
$\angle ACE =\frac {1}{2} \times \angle AOE =\frac {1}{2}\times 180^o=90^o$
kemudian perhatikan $\angle ABC$ dan $\angle AEC$. Kedua sudut tersebut menghadap busur yang sama yakni $\overset{\frown}{AC}$. Maka berdasarkan sifat semua sudut keliling yang menghadap busur yang sama, kita dapatkan
$\angle ABC = \angle AEC$
Dengan demikian kita dapat menyimpulkan bahwa $\bigtriangleup ABD$ sebanding dengan $\bigtriangleup AEC$ sehingga berlaku hubungan perbandingan yakni:
$\displaystyle \frac{AE}{AB}=\frac {AC}{AD}$
$\displaystyle \frac{2r}{c}=\frac {b}{AD}$ $\Leftrightarrow$ sebab AE adalah diameter lingkaran
$\displaystyle AD=\frac {b\times c}{2r}$ ............... persamaan (i)
Sekarang kita amati kembali $\bigtriangleup ABC$. Dengan mensubtitusikan persamaan (i) maka kita dapatkan luas segitiga tersebut adalahLuas $\displaystyle \bigtriangleup ABC = \frac{1}{2} \times BC \times AD=\frac{1}{2}\times a \times \left ( \frac{b \times c}{2r} \right ) = \frac{a\times b \times c}{4r}$
atau
$\displaystyle r = \frac {a \times b \times c}{4 \times \begin {matrix} luas & \bigtriangleup ABC \end {matrix}}= \frac {a \times b \times c}{4 \sqrt{s(s-a)(s-b)(s-c)}}$
untuk $\displaystyle s=\frac{1}{2} \times (a+b+c)$
Dengan demikian kita dapat menyimpulkan bahwa
"Panjang jari-jari lingkaran luar segitiga sama dengan hasil perkalian sisi-sisi segitiga dibagi dengan 4 kali luas segitiga tersebut, yakni :
$\displaystyle r = \frac {a \times b \times c}{4 \times \begin {matrix} luas & \bigtriangleup ABC \end {matrix}}= \frac {a \times b \times c}{4 \sqrt{s(s-a)(s-b)(s-c)}}$
untuk $\displaystyle s=\frac{1}{2} \times (a+b+c)$
===== Selamat Belajar =====