Pembahasan tugas : Jari-jari lingkaran dalam dan luar segitiga

 Latihan Soal: 
Jari-Jari Lingkaran Dalam dan Luar Segitiga

dikumpulkan pada 29 Januari 2022

Kerjakan soal berikut dengan baik dan benar

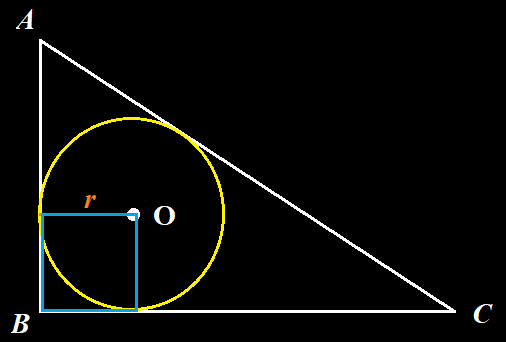
1. Perhatikan gambar berikut ini.
   
   
   
   
   
   Jika panjang AB = 8 cm, BC = 9 cm, dan AC $= \sqrt{145}$ cm, tentukan
          a. luas  ABC;
          b. keliling  ABC;
          c. panjang jari-jari lingkaran dalam segitiga ABC.
   
   Jawab:
   
   a. Karena $\bigtriangleup ABC$ merupakan segitiga siku-siku maka berlaku
   
   
   Luas $\displaystyle \bigtriangleup ABC= \frac{1}{2}\times BC \times AB = \frac{1}{2}\times 9 \times 8 = 36$ cm$^2$
   
   b, Keliling $\bigtriangleup ABC = AB + BC + AC = 8 + 9 + \sqrt{145}=17 + \sqrt{145}$
   
   
   c. panjang jari-jari lingkaran dalam $\bigtriangleup$ 
   
   
   $\displaystyle r = \frac{\begin {matrix}luas & \bigtriangleup ABC \end {matrix}}{s}=\frac{36}{\frac{1}{2}\times \begin {matrix}keliling & \bigtriangleup ABC\end {matrix}}=\frac{36}{\frac {1}{2}\times(17+\sqrt{145})}=\frac{72}{17+\sqrt {145}}$ 
   
   
   
2. Perhatikan gambar berikut ini!
   
   
   
   
   
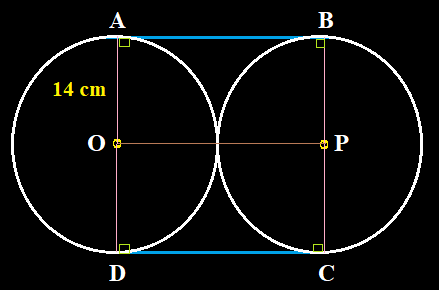
   diketahui panjang AB = BC = AC = 9 cm. Tentukan 
           a. luas ' ABC;
           b. panjang jari-jari lingkaran luar ' ABC. 
   
   Jawab
   
   a. $\displaystyle s =\frac{1}{2}\times (AB+BC+AC) =\frac {1}{2}\times 3 \times 9 = \frac{27}{2}$ cm
   
           luas $\displaystyle \bigtriangleup ABC =\sqrt{s(s-AB)(s-BC)(s-AC)}=\sqrt{ \frac{27}{2}\times  ( \frac{27}{2}-9)^3}$
   
           luas $\displaystyle \bigtriangleup ABC=\sqrt{ \frac{27}{2}\times  \left ( \frac{9}{2} \right )^3}=\frac{27}{2}=\frac{81}{4}\sqrt 3$ cm$^2$
   
   
   
   b. Panjang jari-jari lingkaran luar $\bigtriangleup ABC$
   
   
   $\displaystyle r =\frac{AB\times BC\times AC}{4\times \begin {matrix} luas & \bigtriangleup ABC \end {matrix}}=\frac{3\times 9}{\frac {81}{4} \sqrt 3}=\frac{4}{3\sqrt 3}=\frac{4\sqrt 3}{9}$ cm
   
   
   
   
3. Panjang sisi miring suatu segitiga siku-siku adalah 26 cm dan panjang salah satu sisi siku-sikunya 10 cm. Tentukan
           a. panjang jari-jari lingkaran dalam segitiga;
           b. panjang jari-jari lingkaran luar segitiga.
   
   Jawab
   
   
   a = 10, c = 26 dan  b = ? .Gunakan phytagoras untuk mencari b
   
   
   $b=\sqrt {c^2-a^2}=\sqrt{26^2-10^2}=\sqrt{676-100}=\sqrt{576}=24$
   
   
   Luas segitiga $\displaystyle =\frac{1}{2}\times a \times b = \frac{1}{2} \times 10 \times 24 = 120$ cm$^2$
   
   
   $\displaystyle s = \frac{1}{2}(a + b + c)=\frac{1}{2}(10+24+26)=30$   
   
   a. $\displaystyle r =\frac {luas \bigtriangleup}{s}=\frac{120}{30}=4$ cm
   
   b. $\displaystyle r =\frac{a\times b \times c}{4\times luas \bigtriangleup}=\frac{10\times 24\times 26}{4 \times 120}=13$ cm
   
   
   
4. Panjang sisi-sisi sebuah segitiga adalah 26 cm, 28 cm, dan 38 cm. Hitunglah
           a. panjang jari-jari lingkaran dalam segitiga;
           b. panjang jari-jari lingkaran luar segitiga.
   
   Jawab:
   
   
   $a=26, b=28$ dan $c=38$
   $\displaystyle s=\frac{1}{2}(a+b+c)=\frac{1}{2}(26+28+38)=46$
   
   
   luas $\bigtriangleup =\sqrt {s(s-a)(s-b)(s-c)}=\sqrt{46(46-26)(46-28)(46-38)}=\sqrt{46\times 20\times 18 \times 8}=24\sqrt {230} $ cm$^2$
   
   a. panjang jari-jari lingkaran dalam segitiga =
   
   
   $\displaystyle r =\frac {luas \bigtriangleup}{s}=\frac{24 \sqrt{230}}{46}=\frac{12 \sqrt 230}{23}$ cm
   
   b. Panjang jari-jari lingkaran luar segitiga =
   
   
   $\displaystyle r =\frac {a \times b \times c}{4\times luas \bigtriangleup}=\frac{26\times 28 \times 38}{4 \times 24 \sqrt{230}}=\frac{1729 \sqrt 230}{1380}$ cm
   
   
   
5. Panjang sisi-sisi sebuah segitiga adalah 8 cm, 15 cm, dan 17 cm. Hitunglah
           a. panjang jari-jari lingkaran dalam segitiga;
           b. panjang jari-jari lingkaran luar segitiga
   
   jawab:
   
   Jawab:
   
   
   $a= 8, b=15$ dan $c=17$
   
   
   $\displaystyle s=\frac{1}{2}(a+b+c)=\frac{1}{2}(8+15+17)=20$
   
   
   luas $\bigtriangleup =\sqrt {s(s-a)(s-b)(s-c)}=\sqrt{20(20-8)(20-15)(20-17)}=\sqrt{20\times 12\times 5 \times 3}=60 $ cm$^2$
   
   
   
   a. Panjang jari-jari lingkaran dalam segitiga =
   
   
   $\displaystyle r =\frac {luas \bigtriangleup}{s}=\frac{60}{20}=3$ cm
   
   b. Panjang jari-jari lingkaran luar segitiga =
   
   
   $\displaystyle r =\frac {a \times b \times c}{4\times luas \bigtriangleup}=\frac{8\times 15 \times 17}{4 \times 60}=8,5$ cm

==== Selamat Mengerjakan ====

catatan:
Sebagai bahan acuan untuk mengerjakan soal tersebut, dapat kalian baca pada tautan berjudul "Menentukan panjang jari-jari lingkaran dalam dan luar segitiga"

Jari-jari lingkaran dalam dan luar segitiga.

Menentukan Panjang Jari - Jari Lingkaran Dalam dan Luar Segitiga

Setelah kita membahas materi tentang sabuk pada lingkaran, kali ini kita akan mempelajari materi mengenai bagaimana menentukan panjang jari-jari lingkaran dimana tiga titik pada lingkaran tersebut masing-masing menyinggung sisi-sisi pada segitiga. Pada pembahasan kali ini. kita akan mengenal istilah jari-jari lingkaran dalam segitiga dan jari-jari lingkaran luar segitiga. Namun sebelum kita mengenal lebih jauh mengenai hal itu, kita akan diperkenalkan terlebih dahulu teknik menghitung luas segitiga bila diketahui panjang ketiga sisinya.

A. Menentukan Luas Segitiga Bila Diketahui Panjang Sisi-Sisinya.

 Perhatikan gambar berikut ini:

Gambar di atas menunjukan bahwa segitiga $\bigtriangleup ABC$ memiliki panjang sisi AB = c, AC = b dan BC = a. Jika kita menarik garis tegak lurus BC dan melalui A, maka akan didapatkan titik potong garis tegak lurus tersebut dengan garis BC. Misalkan saja titik potong tersebut adalah D. Apabila kita andaikan panjang BD = x, maka panjang CD = a - x. Dengan demikian berdasarkan rumus Phtagoras kita dapatkan:

$t^2 = c^2 - x ^2$   dan  $t^2 = b^2 - (a-x)^2$ ........ persamaan 1

jika kita subtitusikan kedua persaman tersebut maka kita akan mendapatkan   

                $c^2 - x ^2 = b^2 - (a-x)^2$ 

                $c^2 - x ^2 = b^2 - a^2+2ax- x^2$

                $c^2 - b ^2 + a^2= 2ax$

                $\displaystyle x = \frac {c^2 - b ^2 + a^2}{2a}$

kita subtitusikan persamaan terakhir ke dalam bagian pertama persamaan 1 didapat

                 $t^2 = c^2 - x ^2$

                 $\displaystyle t^2 = c^2 - \left ( \frac{c^2-b^2+a^2}{2a} \right) ^2$    ingat      $p^2 - q^2 = (p-q) (p+q)$     

                 $\displaystyle t^2 = \left ( c+\frac{c^2-b^2+a^2}{2a} \right) \left ( c-\frac{c^2-b^2+a^2}{2a}  \right )$

                 $\displaystyle t^2 = \left (\frac{2ac+c^2-b^2+a^2}{2a} \right) \left ( \frac{2ac-(c^2-b^2+a^2)}{2a}  \right )$

                 $\displaystyle t^2 = \left (\frac{c^2-b^2+a^2+2ac}{2a} \right) \left ( \frac{-c^2+b^2-a^2+2ac}{2a}  \right )$

                 $\displaystyle t^2 = \left (\frac{c^2+2ac+a^2-b^2}{2a} \right) \left ( \frac{b^2-(c^2-2ac+a^2)}{2a}  \right )$

                 $\displaystyle t^2 = \left (\frac{(c+a)^2-b^2}{2a} \right) \left ( \frac{b^2-(c-a)^2}{2a}  \right )$

                 $\displaystyle t^2 = \left (\frac{(c+a+b)(c+a-b)}{2a} \right) \left ( \frac{(b+c-a)(b-(c-a))}{2a}  \right )$ 

                 $\displaystyle t^2 = \left (\frac{(c+a+b)(c+a-b)}{2a} \right) \left ( \frac{(b+c-a)(b-c+a))}{2a}  \right )$  ..... persamaan 2

Sekarang misalkan $\displaystyle s =\frac {1}{2}\times keliling$ $\displaystyle \bigtriangleup ABC=\frac{1}{2}(a+b+c)$, maka

                 $a+b+c =2s$       $c+a = 2s - b$      $a+b = 2s - c$       $b+c=2s -a$   ..... persamaan 3

Sehingga dari persamaan 2 dan persamaan 3 diperoleh

                $\displaystyle t^2 = \left (\frac{(c+a+b)(c+a-b)}{2a} \right) \left ( \frac{(b+c-a)(b-c+a))}{2a}  \right )$  

               $\displaystyle t^2 = \left (\frac{(s)((2s-b)-b)}{2a} \right) \left ( \frac{((2s-a)-a)((2s-c)-c)}{2a}  \right )$  

               $\displaystyle t^2 = \left (\frac{(2s)(2s-2b)}{2a} \right) \left ( \frac{(2s-2a)(2s-2c)}{2a}  \right )$  

              $\displaystyle t^2 = \left (\frac{2(2s)(s-b)}{2a} \right) \left ( \frac{2(s-a) 2(s-c)}{2a}  \right )$  

              $\displaystyle t^2 = \left (\frac{4(s)(s-b)(s-b)(s-a)}{a^2} \right) $  

              $\displaystyle t = \frac{2}{a}\sqrt{(s)(s-b)(s-b)(s-a) } $  

Karena Luas $\bigtriangleup ABC = \frac {1}{2}\times a \times t$, maka dari persamaan terakhir diperoleh

               Luas $\displaystyle \bigtriangleup ABC = \frac {1}{2}\times a \times \frac{2}{a}\sqrt{(s)(s-b)(s-b)(s-a) }$

               Luas $\bigtriangleup ABC = \sqrt{(s)(s-b)(s-b)(s-a) }$

            

Dengan demikian kita sudah dapat menyimpulkan bahwa

Rumus :
" Jika sebuah segitiga memiliki panjang sisi masing-masing adalah a, b dan c, maka luas segitiga tersebut adalah 

               Luas $=\sqrt {s (s-a)(s-b)(s-c)}$        dimana $\displaystyle s = \frac{1}{2}\times (a+b+c)$

B. Jari-jari Lingkaran  Dalam Segitiga

Sekarang perhatikan gambar berikut ini

Pada gambar di atas nampak a, b, dan c adalah panjang sisi masing-masing segitiga. Setiap sisi segitiga tersebut bersinggungan dengan sebuah lingkaran yang terdapat pada segitiga tersebut. Kita akan menunjukan hubungan antara luas segitiga, panjang sisi segitiga dan jari-jari lingkaran dalam segitiga tersebut.

Perhatikan bahwa segitiga $\bigtriangleup ABC$ terbagi dalam 3 buah segitiga yakni : $\bigtriangleup AOB. \bigtriangleup AOC$  dan  $\bigtriangleup BOC$. Jari-jari lingkaran yang terdapat di dalam $\bigtriangleup ABC$  merupakan tinggi dari setiap segitiga tersebut. Dengan demikian 

Luas $\bigtriangleup ABC =$ luas $\bigtriangleup AOB$ + luas $\bigtriangleup AOC$ + luas $\bigtriangleup BOC$

                   Luas $\displaystyle \bigtriangleup ABC =\frac {1}{2}. c . r + \frac {1}{2}.b.r + \frac{1}{2}.a.r$

                   Luas $\displaystyle \bigtriangleup ABC =\frac {1}{2} r . (a+b + c)$

karena (a+b+c) = 2s dan luas segitiga  $=\sqrt {s(s-a)(s-b)(s-c)}$  maka kita dapatkan 

                   Luas $\displaystyle \bigtriangleup ABC =\frac {1}{2} r . (a+b + c)$

                   Luas $\displaystyle \bigtriangleup ABC =\frac {1}{2} r . 2s$


                   $\displaystyle r= \frac {\begin {matrix} luas&\bigtriangleup ABC \end {matrix}}{s}=\frac{\sqrt {s(s-a)(s-b)(s-c)}}{s}$

Dengan demikian kita dapat menyimpulkan bahwa

"Panjang jari-jari lingkaran dalam segitiga sama dengan luas segitiga dibagi setengah dari keliling segitiga, yakni:

  $\displaystyle r= \frac {\begin {matrix} luas&\bigtriangleup ABC \end {matrix}}{s}=\frac{\sqrt {s(s-a)(s-b)(s-c)}}{s}$

C. Jari-jari Lingkaran Luar Segitiga

Untuk memahami jari-jari lingkaran luar segitiga, kalian bisa mengamti gambar berikut ini:

Gambar di atas menunjukan bahwa sebuah segitiga $\bigtriangleup ABC$ berada di dalam lingkaran yang berjari-jari. Setiap sudut dari $\bigtriangleup ABC$ menyinggung lingkaran yang berpusat di O. Panjang sisi $AB =c , BC = a$ dan $AC = b$. Kita akan menentukan apakah ada hubungan antara jari-jari lingkaran dengan panjang ketiga sisi segitiga tersebut. Sebagai gambaran awalny, coba kalian membuat garis AD yang tegak lurus dengan garis BC. Kemudian kalian buat perpanjangan garis AO sampai memotong lingkaran di titik E. Maka kalian akan mendapati gambar seperti berikut ini:

 

Kalau kalian amati, AE merupakan diameter lingkaran dan $\angle ACE$ merupakan sudut keliling yang menghadap busur $\overset{\frown}{AE}$.  Berdasarkan sifat sudut keliling dan sudut pusat,  maka kita dapatkan:

$\angle ACE =\frac {1}{2} \times \angle AOE =\frac {1}{2}\times 180^o=90^o$

kemudian perhatikan $\angle ABC$ dan $\angle AEC$. Kedua sudut tersebut menghadap busur yang sama yakni $\overset{\frown}{AC}$. Maka berdasarkan sifat semua sudut keliling yang menghadap busur yang sama, kita dapatkan

$\angle ABC = \angle AEC$

Dengan demikian kita dapat menyimpulkan bahwa $\bigtriangleup ABD$ sebanding dengan $\bigtriangleup AEC$ sehingga berlaku hubungan perbandingan yakni:

$\displaystyle \frac{AE}{AB}=\frac {AC}{AD}$

$\displaystyle \frac{2r}{c}=\frac {b}{AD}$      $\Leftrightarrow$   sebab AE adalah diameter lingkaran

$\displaystyle AD=\frac {b\times c}{2r}$  ............... persamaan (i)

Sekarang kita amati kembali $\bigtriangleup ABC$. Dengan mensubtitusikan persamaan (i) maka kita dapatkan luas segitiga tersebut adalah

Luas $\displaystyle \bigtriangleup ABC = \frac{1}{2} \times BC \times AD=\frac{1}{2}\times a \times \left ( \frac{b \times c}{2r} \right ) = \frac{a\times b \times c}{4r}$

atau

$\displaystyle r = \frac {a \times b \times c}{4 \times \begin {matrix} luas & \bigtriangleup ABC \end {matrix}}= \frac {a \times b \times c}{4 \sqrt{s(s-a)(s-b)(s-c)}}$

untuk  $\displaystyle s=\frac{1}{2} \times (a+b+c)$

Dengan demikian kita dapat menyimpulkan bahwa
"Panjang jari-jari lingkaran luar segitiga sama dengan hasil perkalian sisi-sisi segitiga dibagi dengan 4 kali luas segitiga tersebut, yakni :

$\displaystyle r = \frac {a \times b \times c}{4 \times \begin {matrix} luas & \bigtriangleup ABC \end {matrix}}= \frac {a \times b \times c}{4 \sqrt{s(s-a)(s-b)(s-c)}}$

untuk  $\displaystyle s=\frac{1}{2} \times (a+b+c)$

===== Selamat Belajar =====

Menentukan panjang sabuk lingkaran

Kalian tentu tahu rantai sepeda bukan? ya... rantai sepeda merupakan bagian dari sepeda yang digunakan sebagai penggerak sepeda. Nah, apakah kalian dapat menghitung panjang rantai sepeda jika diketahui panjang jari-jari gear sepeda? Pada pembahasan kali ini kita akan diperkenalkan contoh penyelesaian bagaimana menghitung panjang sabuk lingkaran. Dengan kalian mengetahui bagaimana langkah-langkah perhitungannya, kalian akan dapat menentukan sendiri panjang rantai sepeda.

Contoh 1

Dua buah gear sepeda memiliki jari-jari sama sebesar 14 cm. Tentukan panjang rantai yang menghubungkan gear speda tersebut!

jawab  
perhatikan gambar berikut

Pada gambar di atas kita mengetahui bahwa dua gear memiliki jari-jari yang sama yakni 14 cm. Dengan demikian panjang $AB = CD = 2\times 14 = 28$ cm. Busur $\overset {\frown}{AD}=\overset {\frown}{BC}$. Kita akan menentukan panjang busur tersebut untuk mengetahui panjang rantai yang mengelilingi gear 1 dan gear 2.

Perhatikan bahwa busur $\overset AD$ merupakan $\frac{1}{2}$ keliling lingkaran. Karena busur Busur $\overset {\frown}{AD}=\overset {\frown}{BC}$ , Maka jelas bahwa jumlah panjang rantai yang mengelilingi gear 1 dan gear 2 tidak lain adalah keliling 1 buah gear itu sendiri. Sehingga kita dapatkan

panjang sabuk = keliling lingkaran  $+ AB + CD \displaystyle = \pi \times diameter + 28 + 28 = \frac {22}{7} \times 28 + 56 = 88 + 56 = 144$ cm

Jadi panjang rantai yang dibutuhkan adalah 144 cm  

Contoh 2

Diketahui 3 buah lingkaran memiliki jari-jari 7 cm diikat sedemikian rupa seperti gambar berikut ini:

Hitunglah panjang tali yang dibutuhkan untuk mengikat ke tiga lingkaran tersebut!

Jawab:
perhatikan gambar berikut ini

Ketiga lingkaran masing-masing memiliki titik pusat di A, B dan C. Karena masing-masing lingkaran memiliki jari-jari 7 cm, maka  panjang AB = BC = AC = 7 +7 =14 cm. $\bigtriangleup ABC$ merupakan segitiga sama sisi, sehingga $\angle ABC = \angle BCA = \angle BAC = 60^o$. Selain itu karena letaknya yang kosentris terhadap segitiga sama sisi ABC, maka panjang busur $\overset{\frown}{DI}=\overset{\frown}{UF}=\overset{\frown}{GH}$, Kita akan menentukan panjang masing busur ini untuk menentukan panjang tali yang melingkari masing-masing lingkaran.

Perhatikan lingkaran yang berpusat di A
karena ABDE, BCGF dan  ACHI adalah persegi panjang maka $\angle DAB = \angle IAC=90^2$ dan  = AB = 14
Dengan demikian kita dapat menentukan besar sudut $\angle DAI$ yakni
$\angle DAI =360^o - \angle DAB - \angle IAC - \angle BAC=360^o-90^o-90^o-60^o=120^o$ 

Berdasarkan teori garis singgung lingkaran, maka kita dapatkan

Panjang busur $\displaystyle \overset{\frown}{DI}= \frac{\angle DAI}{360^o}\times \begin {matrix} keliling&lingkaran&A \end {matrix}=\frac {120^o}{360^o}\times \frac {22}{7}\times 14=\frac {1}{3}\times 44=\frac {44}{3}$ cm

Dengan demikian panjang sabuk ketiga lingkaran tersebut dapat kita cari, yakni

Panjang sabuk  $=\overset{\frown}{DI}+\overset{\frown}{UF}+\overset{\frown}{GH}+ DE + FG + HI$
        $\Leftrightarrow$           $\displaystyle = 3 \times (\overset{\frown}{DI} + AB) = 3 \times (\frac {44}{3}+14)=44 +42=86$ cm

Jadi panjang tali yang dibutuhkan $\geq$ dari 86 cm.

Contoh 3

Gambar di atas adalah penampang enam buah drum yang berbentuk tabung dengan jari-jari 24 cm. Hitunglah panjang tali minimal yang diperlukan untuk mengikat enam buah drum tersebut.

Jawab:
sama seperti pada contoh 2, keenam lingkaran tersebut tersusun secara konsentris terhadap segitiga sama sisi yang panjang sisinya $= 4 \times 24 = 96$ cm. Karena kedudukannya yang konsentris maka besar sudut yang terbentuk pada busur yang dikeliling tali (lingkaran 1, 4 dan 6) sebesar $120^o$. Dengan demikian

panjang busur $=3 \times$ panjang sisi segitiga sama sisi + $3 \times$ panjang busur yang dikeliling tali $ =3 \times 96 + 3 \times \frac {120^o}{360^o}\times 3,14 \times 48 =288 +150,72= 438,72$ cm

==== Selamat Belajar ====

Pembahasan Tugas harian 1: garis singgung lingkaran kelas 8 SMP (27 Januari 2022)

Latihan Soal Garis Singgung Lingkaran
Kelas 8 SMP 

Tugas dikumpulkan pada 27 Januari 2022

dikirim langsung melalui alamat email: altissimastudycenter@gmail.com

Kerjakan soal berikut dengan benar

1. Dari garis-garis k, l, m, n, dan p pada gambar di atas, manakah yang merupakan garis singgung lingkaran? 
   
   
   
   
   jawab:
   
   Salah satu ciri khas garis singgung lingkaran adalah tidak memotong lingkaran di dua titik tetapi menyentuh lingkaran di satu titik. Oleh karena itu garis yang menyinggung lingkaran pada gambar tersebut adalah garis l, garis n dan garis j.
   
   
2. Lukislah pada kertas berpetak lingkaran berpusat di titik O(0, 0) dengan jari-jari 5 satuan panjang. Selanjutnya lukislah garis singgung lingkaran yang melalui titik A(0, 5). 
   
   jawab
   
   

   
   
   
   
3. Lukislah pada kertas berpetak lingkaran dengan pusat di titik P(3, 2) dan jari-jari 4 satuan panjang. Selanjutnya, lukislah garis singgung lingkaran yang melalui titik Q(–1, 2).
   
   jawab :
   
   
   

   
   
   
4. Berdasarkan keterangan pada gambar berikut, hitunglah panjang setiap garis singgung lingkarannya.
   
   
   
   
   jawab
   
   (i)   $AB=\sqrt{OB^2-OA^2}=\sqrt{7^2-5^2}=\sqrt{49-25}=\sqrt{24}=2\sqrt 6$  cm
   
   (ii)  $PQ=\sqrt{OP^2-OQ^2}=\sqrt{20^2-12^2}=\sqrt{400-144}=\sqrt{256}=16$  cm
   
   (iii) $XY=\sqrt{OX^2-OY^2}=\sqrt{26^2-10^2}=\sqrt{676-100}=\sqrt{576}=24$  cm
   
   
5. Perhatikan gambar berikut:
   
   
   
   
   
   Garis AB dan BC adalah garis singgung lingkaran yang melalui titik A. Jika OA = 10 cm dan OB = 26 cm maka tentukan
             a. panjang garis singgung AB;
             b. luas layang-layang OBAC;
             c. panjang tali busur AC.
   jawab
   
   a. $AB=\sqrt{OB^2-OA^2}=\sqrt{26^2-10^2}=\sqrt{676-100}=\sqrt{576}=24$  cm
   
   b. Luas $\displaystyle \bigtriangleup OAB=\frac{1}{2} \times AB \times OA= \frac{1}{2}\times 24 \times 10 = 120$ cm$^2$
   
       Jadi luas layang-layang $= 2\times \bigtriangleup OAB = 2 \times 120=240$ cm$^2$
   
   c. Misalkan D adalah titik potong diagonal layang-layang
       Dengan menggunakan perbandingan luas kita dapatkan 
   
       Luas $\displaystyle \bigtriangleup OAB=\frac{1}{2} \times OB \times AD$
   
       $\displaystyle 120 =\frac{1}{2} \times 26 \times AD$
   
       $\displaystyle AD =\frac{120}{13} $
        
       dengan demikian panjang tali busur layang $\displaystyle AC = 2 \times AD = 2 \times \frac {120}{13} = \frac {240}{13}$ cm 
   
   
6. Perhatikan gambar berikut.
   
   
   
   
   Berdasarkan gambar tersebut, benar atau salahkah pernyataan-pernyataan berikut?
         a. AB sejajar PQ
         b. AP tegak lurus PQ 
         c. AB = CD
         d. AB = PQ
         e. AP tegak lurus AB di titik A
   
   jawab:
   a. salah karena $\angle PAB \neq \angle APQ$ dan $\angle ABQ \neq \angle PQB$
   b. Benar berdasarkan sifat garis singgung lingkaran.
   c. Benar berdasarkan sifat garis singgung persekutuan luar lingkaran 
   d. Salah karena AB adalah ruas garis singgung persekutuan luar lingkaran, sedangkan PQ jarak titik pusat kedua lingkaran. berdasarkan sifat garis singgung persekutuan luar panjang PQ > panjang AB 
   
   
7. Panjang jari-jari dua lingkaran masing-masing adalah 12 cm dan 5 cm. Jarak kedua titik pusatnya adalah 24 cm. Hitunglah
         a. panjang garis singgung persekutuan dalam;
         b. panjang garis singgung persekutuan luarnya.
   
   Jawab
   diketahui  p = 24, R = 12 dan r = 5
   a. $d = \sqrt{p^2-(R+r)^2}=\sqrt{24^2-(12+5)^2}=\sqrt{576 - 289}=\sqrt {287}$ cm
   
   b. $d =\sqrt{p^2-(R-r)^2}=\sqrt{24^2-(12-5)^2}=\sqrt{576 - 49}=\sqrt {527}$ cm
   
   
8. Perhatikan gambar di atas.
   
   
   
   
   
   Panjang jari-jari lingkaran yang berpusat di O adalah 9 cm dan panjang jari-jari lingkaran yang berpusat di P adalah 4 cm. Jika panjang garis singgung persekutuan luarnya 12 cm, tentukan
         a. jarak kedua pusat lingkaran;
         b. luas segi empat yang diarsir
   
   Jawab
   
   Diketahui d = 12 cm, R = 9 cm dan r = 4 cm 
   
   a. $p = \sqrt {d^2+(R-r)^2}=\sqrt{12^2+(9-4)^2}=\sqrt{144 + 25}=\sqrt {13}$ cm
   b. Luas daerah yang diarsir $=2 \times \begin {matrix} luas & trapesium \end {matrix}= 2\times \frac{1}{2}\times (R+r) \times AB=2 \times \frac{1}{2} \times (9+4)\times 12 =156$ cm$^2$
   
   
9. Panjang garis singgung persekutuan dalam dua lingkaran adalah 24 cm dan jarak kedua pusatnya adalah 26 cm. Jika panjang salah satu jari-jari lingkaran 6 cm, hitunglah panjang jari-jari lingkaran yang lain. 
   
   Jawab
   diketahui d = 24 cm, p =26 cm dan  R = 6 cm
   $R + r = \sqrt{p^2 - d^2}$
   $ 6 + t = \sqrt{26^2-6^2}=\sqrt{676-576}=\sqrt{100}=10$    $\Leftrightarrow$   $r =10-6=4 cm$
    
10. Panjang jari-jari dua buah lingkaran yang berpusat di O dan P masing-masing adalah 8 cm dan 4 cm. Jarak kedua titik pusatnya 20 cm.
       a. Lukislah garis singgung persekutuan dalamnya.
       b. Hitunglah panjang garis singgung persekutuan dalam tersebut.

Jawab
diketahui  R = 8 cm, r = 4 cm dan p = 20 cm

a, 



b. $d = \sqrt{p^2-(R+r)^2}=\sqrt{20^2-(8+4)^2}=\sqrt{400 - 144}=\sqrt {256}=16$ cm

Bahan acuan untuk mengerjakan soal ini:

• Kharakteristik garis singgung lingkaran
• Garis singgung persekutuan lingkaran