Pembahasan Soal Bangun ruang

 Kerjakan soal berikut dengan baik dan benar

1. Banyaknya titik sudut pada prisma segitiga adalah ....
             a.   6 buah                     
             b. 10 buah
             c.   8 buah
             d. 12 buah
   
   Jawab:
   
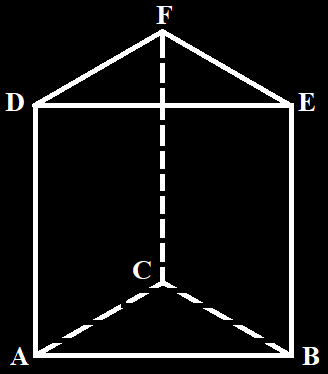
   Perhatikan gambar di bawah ini :
   
   
   
   
   Dengan demikian nampak bahwa jumlah sudut prisma segitiga adalah 6 buah.
   
   
2. Banyaknya rusuk alas pada limas segi empat adalah ....
             a. 3 buah
             b. 7 buah
             c. 4 buah
             d. 8 buah
   
   
3. Perhatikan gambar prisma segi lima beraturan berikut ini.
   
   
   
   
   
   Pernyataan di bawah ini benar, kecuali ....
             a. rusuk-rusuk tegaknya adalah KP, LQ, MR, NS, dan OT
             b. bidang KLMNO kongruen dengan bidang PQRST
             c. bidang KMRP dan KNSP merupakan bidang diagonal
             d. diagonal bidang alasnya ada 4 buah
   
   Jawab :
   Jawaban yang salah adalah (d) sebab jumlah diagonal alasnya adalah 5  buah. yakni: OL, OM, KM, KN, dan LN.
   
   
   
   
   
    
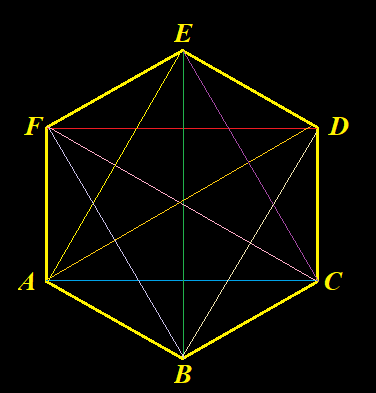
4. Gambar di bawah ini merupakan jaring - jaring ....
   
   
   
   
             a. limas segi lima beraturan
             b. limas segi enam beraturan
             c. prisma segi lima beraturan
             d. prisma segi enam beraturan
   
   Jawab
   Jika melihat segilima sebagai alasnya dan kelima segitiga sebagai sisi tegaknya, maka bangun ruang yang terbentuk adalah limas segilima beraturan.
   
   
   
   
   
   
   
5. Suatu prisma alasnya berbentuk segitiga dengan panjang sisi 3 cm, 4 cm, dan 5 cm. Jika tinggi prisma 15 cm, volume prisma adalah ....
              a.   90 cm$^3$
              b. 250 cm$^3$
              c. 200 cm$^3$
              d. 300 cm$^3$ 
   
   Jawab
   
   jika melihat ukuran panjang sisi segitiga alasnya, maka segitiga tersebut memenuhi syarat phytagoras dengan kedua sisi siku-sikunya memiliki panjang 3 cm dan 4 cm. Dengan demikian volume prisma segitiga adalah
   
   

   Volume prisma = luas alas $\times$ tinggi prisma = $\displaystyle \left (\frac {1}{2} \times 3 \times 4 \right ) \times 15 = 90$ cm$^3$ 
   
   
6. Diketahui luas permukaan prisma tegak segi empat beraturan 864 cm$^2$ dan tinggi prisma 6 cm. Panjang sisi alas prisma adalah ....
              a. 8 cm
              b. 12 cm
              c. 10 cm
              d. 14 cm
   
   Jawab
                Volume prisma = luas alas $\times$ tinggi prisma = $\displaystyle s \times s \times 12 $
   
                 $\Leftrightarrow$    $\displaystyle s^2= \frac {864}{6} = 144$
   
                 $\Leftrightarrow$    $\displaystyle s= \sqrt {144}=12$ cm
   
   
   
7. Diketahui suatu limas dengan alas berbentuk persegi. Luas alas limas 144 cm2 dan tinggi limas 8 cm. Luas permukaan limas adalah ....
               a. 204 cm$^2$
               b. 484 cm$^2$ 
               c. 384 cm$^2$ 
               d. 1.152 cm$^2$
   
   jawab
   
   
   
   
   
   Sisi alas limas  = $ \sqrt ($luas alas) $ =\sqrt {144}=12$ cm
   
   tinggi sisi tegak limas = $\sqrt {6^2 + 8^2}=10$ cm
   
   Dengan demikian luas permukaan limas tersebut =
   
   Luas limas segiempat beraturan = 4 $\times$ luas segitiga + luas alas
   
                                                       = $\displaystyle 4 \times \frac {1}{2} \times 12 \times 10 $ + 144
   
                                                       =              240           + 144 
   
                                                       = 384 cm$^2$
          
8. Diketahui volume suatu prisma 450 cm$^3$. Alas prisma berbentuk segitiga siku-siku dengan panjang sisi 5 cm, 13 cm, dan 12 cm. Tinggi prisma adalah ....
               a. 12 cm
               b. 14 cm
               c. 13 cm
               d. 15 cm
   
   Jawab
   Karena sisi terpanjang segitiga berukuran 13 cm maka sisi tegaknya berukuran 5 cm dan 12 cm
   
   Volume Prisma  = luas alas $\times$ tinggi prisma
            450           $\displaystyle \frac {1}{2}\times 5 \times 12 \times$ tinggi prisma
   
            450           $ = 30 \times$ tinggi prisma
   
   $\Leftrightarrow$   tinggi prisma $\displaystyle =\frac {450}{30}=15$ cm
    
9. Jika suatu limas luas alasnya 240 cm$^2$ dan tinggi 30 cm maka volume limas adalah ....
               a. 2.400 cm$^3$
               b. 4840 cm$^3$ 
               c. 4.400 cm$^3$ 
               d. 7.200 cm$^3$ 
   
   Jawab
   
   Volume limas $=\displaystyle \frac {1}{3} \times$ luas alas $\times$ tinggi limas
   
   Volume limas $=\displaystyle \frac {1}{3} \times 240 \times 30 = 2400$ cm$^3$ 
   
   
   
10. Suatu limas memiliki alas berbentuk persegi panjang dengan ukuran 25 cm dan 15 cm. Jika tinggi limas 7 cm, volume limas adalah ....
                a. 262,5 cm$^3$ 
                b. 870 cm$^3$ 
                c. 484 cm$^3$ 
                d. 875 cm$^3$
    
    Jawab
    
    Volume limas $=\displaystyle \frac {1}{3} \times$ luas alas $\times$ tinggi limas
    
    Volume limas $=\displaystyle \frac {1}{3} \times 25\times 15 \times 7=875$ cm$^3$
    
     
    
11. Diketahui prisma tegak segitiga ABC.DEF dengan AB = 15 dm, BC = 12 dm, dan AC = 9 dm.
    
    

    

    
    Jika tinggi prisma itu 2 dm, volumenya adalah ....
                a. 108 liter
                b. 540 liter
                c. 216 liter
                d. 1.080 liter 
    
    Jawab
    alas prisma berbentuk segitiga siku-siku karena memenuhi syarat phytagoras. Dengan demikian sisi yang saling tegak lurus adalah yang berukuran 9 cm dan 12 cm.
    
    Volume prisma = luas alas $\times$ tinggi prisma
    
    Volume limas $\displaystyle \frac {1}{2}\times 9 \times 12 \times 2 = 108$ dm$^3 = 108$ liter
    
    
    
12. Pada prisma tegak segi empat ABCD.EFGH, sisi alas ABCD berupa trapesium sama kaki dengan AB//CD, AB = 10 cm, CD = 4 cm, dan AD = 5 cm. Jika luas semua sisi tegaknya 216 cm$^2$ maka volume prisma itu adalah ....
                a. 252 cm$^3$
                b. 560 cm$^3$
                c. 320 cm$^3$
                d. 600 cm$^3$
    
    Jawab
    
    

    
    
    Pada gambar nampak bidang ADHE sebangun dengan bidang BCGF. Dengan demikian
    Luas selimut = 2 $\times$ luas ADHE + luas CDHG + luas ABFE
           216         $=2 \times 5 \times$ tinggi prisma + $4 \times$ tinggi prisma + $10 \times $ tinggi prisma
           216         $= (10 + 4 + 10) \times$ tinggi prisma    
           216         $= 24 \times$ tinggi prisma 
    
    Tinggi prisma $\displaystyle =\frac{216}{24}=9$ cm
    
    Sekarang perhatikan $\bigtriangleup BCE$ pada trapesium ABCD seperti gambar berikut
    
    
    

    
    
    Dengan demikian tinggi trapesium dapat kita cari dengan menggunakan phytagoras yakni
    
    $BE =\sqrt{BC^2-EC^2}=\sqrt{5^2-3^2}=4$ cm
    
    Volume prisma = luas alas $\times$ tinggi prisma
    
    Volume prisma $\displaystyle =\left ( \frac{DC+AB}{2}\times BE \right ) \times 9 $ 
    
    Volume prisma $\displaystyle =\left ( \frac{10+4}{2}\times 4\right ) \times 9 = 252$ cm$^3$ 
      
    
    
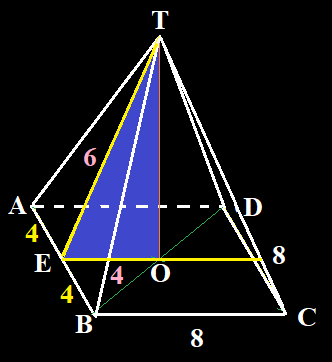
13. Diketahui limas segi empat beraturan T.ABCD, dengan AB = 8 cm dan luas bidang TAB = 24 cm$^2$. Volume limas itu adalah ...
                 a. 94,3 cm$^3$
                 b. 95,4 cm$^3$
                 c. 94,5 cm$^3$
                 d. 96 cm$^3$ 
    
    Jawab
    Perhatikan $\bigtriangleup TAB$ bangun ruang TABCD berikut ini
    
    
    
    
    
    Luas $\bigtriangleup {TAB}\displaystyle =\frac {1}{2}\times AB \times tinggi_{\bigtriangleup {TAB}}$
    
          24       $\displaystyle = \frac {1}{2} \times 8 \times tinggi_{\bigtriangleup TAB}$
    
          24       $\displaystyle = 4 \times tinggi_{\bigtriangleup TAB}$
    
    
    Tinggi$_{\bigtriangleup TAB}\displaystyle = \frac {24}{4} = 6$ cm
    
    
    Sekarang perhatikan $\bigtriangleup TEO$ pada bangun ruang TABCD seperti gambar berikut
    
    
    
    
    Karena EO $\displaystyle =\frac {BC}{2}=\frac {8}{2}=4$ cm dan TE = 6 cm, maka dengan menggunakan phytagoras diperoleh :
     
                Tinggi limas $=\sqrt {TE^2-EO^2}=\sqrt {6^2-4^2}=\sqrt{20}=2\sqrt 5$
    
    Dengan demikian kita dapat mencari volume limas, yakni :
    
               Volume limas $\displaystyle = \frac {1}{3} \times$ luas alas $\times$ tinggi prisma
    
               Volume limas $\displaystyle = \frac {1}{3} \times 8 \times 8 \times 2 \sqrt 5= \frac {128}{3}\sqrt 5 \approx 95,40$ cm$^3$
    
    
    
14. Alas sebuah prisma berbentuk belah ketupat, dengan salah satu panjang diagonalnya adalah 10 cm dan panjang semua sisi tegaknya adalah 12 cm. Jika volume prisma itu 600 cm3, luas sisi prisma itu adalah ....
                  a. $64 + 5\sqrt  2$  cm$^2$ 
                  b. $72 + 15\sqrt  2$  cm$^2$ 
                  c. $96 + 32\sqrt  2$  cm$^2$ 
                  d. $100 + 240\sqrt  2$  cm$^2$
    
    Jawab
    
    
    
    
    Volume prisma = luas alas $\times$ tinggi prisma
    
             600          = luas alas $times 12$
    
    Luas alas $\displaystyle = \frac {600}{12}=50$ cm$^2$
    
    
    
    
    
    Panjang diagonal alas yang lain $\displaystyle = \frac {2 \times Luas} {diagonal}=\frac{2\times 50}{10}=10$ cm
    
    Panjang sisi belah ketupat $=\sqrt{5^2 + 5^2}=5\sqrt 2$
    
    
    
    
    
    luas permukaan $=2 \times$ luas alas $+ 4 \times$ luas persegi panjang
    
    luas permukaan $=2 \times 50 + 4 \times 5 \sqrt 2 \times 12 = 100 + 240 \sqrt 2$ 
    
    
    
15. Sebuah prisma tegak segitiga luas bidang alasnya 24 cm$^2$ dan luas bidang sisi-sisinya adalah 150 cm$^2$, 120 cm$^2$, dan 90 cm$^2$. Volume prisma itu adalah ....
                  a. 90 cm$^3$
                  b. 220 cm$^3$ 
                  c. 120 cm$^3$ 
                  d. 360 cm$^3$
    
    Jawab
    
    panjang sisi segitiga alasnya masing-masing adalah 6 cm, 8 cm , dan 10 cm
    (anda dipersilahkan untukk membuktikannya ya ...)
    
    
    Dengan demikian tinggi prisma bisa dicari melalui salah satu sisinya. Ambil bidang yang memiliki sisi terpanjang dari segitiga alasnya dan memiliki daerah yang paling luas. Maka lebar bidang tersebut adalah 10 dan luasnya = 150 cm$^2$. Maka tinggi prisma yakni
    
    Tinggi prisma $\displaystyle = \frac {luas}{l}=\frac {150}{10}=15$ cm
    
    maka Volume prisma = luas alas $\times$ tinggi prisma $=24 \times 15= 360$ cm$^3$
      

B. Jawablah pertanyaan berikut ini!

1. Gambarlah prisma segi enam beraturan ABCDEF.GHIJKL. Tentukan
                a. rusuk-rusuk tegaknya;
                b. semua diagonal bidang alas;
                c. semua diagonal ruangnya. 
   
   jawab
   
   
   
   
         a. Rusuk tegak : AG, BH, CI, DJ, EK, dan FL
         b. Diagonal bidang alas = AD, AE, AC, BE, BD, BF, CF, CE, dan DF
   
   

   

   diagonal alas

   
   
   
          c. Diagonal ruang
   
   

   

   diagonal ruang

   
   
   
   
2. Limas segi empat beraturan mempunyai luas alas 256 cm$^2$. Jika tinggi limas 6 cm, tentukan luas permukaan limas tersebut.
   
   Jawab
   
   
   
   
   
          Sisi persegi alas $=\sqrt {256} = 16 $ cm
          Tinggi segitiga TAB $=\sqrt {6^2 +8^2}=10 $ cm
   
   Jadi Luas limas $\displaystyle = 4 \times TAB + ABCD = 4 \times \frac {1}{2}\times 16 \times 10 + 256 =320 + 256 = 576$ cm$^2$
     
3. Diketahui alas sebuah prisma berbentuk segitiga siku-siku dengan panjang sisi siku-sikunya 8 cm dan 6 cm. Jika tinggi prisma 18 cm, tentukan luas permukaan prisma.
   
   Jawab
   
   Luas $\bigtriangleup ABC = \frac{1}{2}\times 8 \times 6 = 24$ cm$^2$
   
   
   
   
   
   Maka luas permukaan prisma tersebut 
   
   Luas $= 2 \times$ luas  $\bigtriangleup ABC$ + Luas ACFD + Luas BCFE + Luas ABED  
   
   Luas $= 2 \times 24 + 6 \times 18 + 8 \times 18 + 10 \times 18 =48+108+144 + 180 = 480$ cm$^2$  
   
   
4. Suatu kolam renang mempunyai ukuran panjang 40 m dan lebar 15 m. Kedalaman air pada ujung yang paling dangkal 1,3 m dan ujung yang paling dalam 2,7 m. Berapa liter volume air dalam kolam renang tersebut?
   
   Jawab
   
   

   

   
   
   Volume Kolam seluruhnya  = luas trapesium $\times$ tinggi prisma
   
                                                $\displaystyle = \frac{2,7+1,3}{2} \times 40 \times 15=1200$ m$^3=1.200.000$ liter  
   
   
5. Suatu limas segi lima beraturan T.ABCDE tampak seperti gambar di bawah ini.
   
   
   
   
   
   Panjang AB = 16 cm, OA = 10 cm, dan tinggi limas 20 cm. Hitunglah
           a. luas alas limas;
           b. volume limas.
   
   jawab:
   
   
   
   
   
   Tinggi $\bigtriangleup OAB = \sqrt{10^2-8^2}= \sqrt{36}=6$
   
   a. luas alas limas $= 5\times \frac {1}{2}\times 16 \times 6= 240$ cm$^2$
   
   b. Volume limas $\displaystyle = \frac{1}{3} \times$ luas alas $\times$ tinggi limas
   
                              $ \displaystyle = \frac {1}{3}\times 240 \times 20 =1600 $ cm$^3$

Ulangan Harian Matematika Kelas 8 SMP: Garis Singgung Lingkaran

Soal Ulangan Harian 
Garis Singgung Lingkaran

Jawaban dikumpulkan paling lambat 4 Februari 2022

Kerjakan latihan soal berikut ini

A. Pilihlah salah satu jawaban yang tepat.

1. Panjang garis singgung lingkaran berjari-jari 6 cm dari titik di luar lingkaran yang berjarak 10 cm dari pusat lingkaran adalah ....
              a. 6,5 cm              b . 7,5 cm            c. 7 cm            d. 8 cm
   
   
2. Dari titik P di luar lingkaran yang berpusat di O dibuat garis singgung PA. Jika panjang jari-jari 20 cm dan jarak AP = 21 cm maka panjang OP adalah ....
              a. 23 cm               b. 28 cm              c. 25 cm          d. 29 cm
   
   
3. Dua lingkaran dengan pusat P dan Q, berjari-jari 7 cm dan 5 cm. Jika jarak PQ = 20 cm maka panjang garis singgung persekutuan dalamnya adalah ....
              a. 12 cm               b. 16 cm              c. 15 cm          d. 24 cm
   
   
4. Perhatikan gambar berikut ini
   

   
   

   

   
   Pada gambar di atas AB dan AC adalah garis singgung lingkaran titik A di luar lingkaran. Jika panjang OC = x cm, AC = y cm, dan OA = z cm panjang BC = ....
   
               a. $\displaystyle \frac{xy}{2}$ cm           b. $\displaystyle \frac{xy}{z}$ cm           c. $\displaystyle \frac{2xy}{z}$ cm           d. $\displaystyle \frac {2z}{xy}$ cm
   
   
   Gambar di bawah ini untuk soal no 5 - 7
    

   

   
   
   
5. Diketahui PA dan PB adalah garis singgung lingkaran. Jika panjang OA = 6 cm, OP = 10 cm maka panjang PA = ....
            a. 11 cm               b. 12 cm                c. 8 cm                d. 9 cm
   
   
6. Luas layang-layang OAPB adalah ....
            a. 46 cm$^2$            b. 48 cm$^2$               c. 45 cm$^2$           d. 50 cm$^2$
   
   
7. Panjang tali busur AB adalah ....
            a. 6,9 cm              b. 6,1 cm               c. 9,5 cm             d. 9,6 cm
   
   
8. Perhatikan gambar di atas.
   
   

   

   
   Panjang tali yang digunakan untuk mengikat dua pipa air berjari-jari 7 cm sebanyak lima kali lilitan adalah ....
                a. 28 cm               b. 62 cm                c. 44 cm                d. 72 cm
   
   
9. Panjang sisi-sisi sebuah segitiga adalah 8 cm, 15 cm, dan 17 cm. Panjang jari-jari lingkaran dalamnya adalah ....
                a. 3 cm                 b. 5 cm                  c. 4 cm                  d. 6 cm 
   
   
10. Panjang sisi miring suatu segitiga sikusiku adalah 35 cm dan panjang salah satu sisi siku-sikunya adalah 21 cm. Panjang jari-jari lingkaran luarnya adalah ....
                 a. 15,5 cm            b. 17,5 cm             c. 16,5 cm             d. 18 cm
    
    
    

B. Jawablah pertanyaan-pertanyaan berikut dengan singkat dan tepat.

1. Panjang jari-jari dua lingkaran adalah 7 cm dan 3 cm. Jika panjang garis singgung persekutuan luarnya 15 cm maka tentukan
        a. jarak kedua pusat lingkaran;
        b. panjang garis singgung persekutuan dalamnya.
   
   
2. Perhatikan gambar berikut:
   
   
   
   
   
   Kedua lingkaran bersinggungan di luar dengan pusat di titik B dan D. Jika AB = 5 cm dan DE = 3 cm, hitunglah panjang
         a. AE;
         b. EF.
         c. CF
   
   
3. Diketahui lingkaran L1 berpusat di O(0, 0), dengan jari-jari r1 = 3 satuan dan L2 pusat di P(6, 6), berjari-jari r2 = 2 satuan.
         a. Gambarlah garis singgung persekutuan dalam L1 dan L2. 
         b. Hitunglah panjang garis singgung persekutuan luar dua lingkaran tersebut.
   
   
4. Diketahui empat tong minyak berbentuk tabung diikat menjadi satu untuk diisi kembali. Susunlah empat tong tersebut agar panjang tali yang digunakan untuk mengikatnya minimal, kemudian hitung pula panjangnya, jika diameter tong 14 cm
   
   
5. Perhatikan gambar berikut ini:
   
   
   
   
   Panjang AB = 28 cm dan AC = 21 cm. Hitunglah
         a. panjang jari-jari OD;
         b. panjang BD;
         c. panjang OB; d. luas  COE.
   
   

==== Selamat Mengerjakan ====

Pembahasan tugas : Jari-jari lingkaran dalam dan luar segitiga

 Latihan Soal: 
Jari-Jari Lingkaran Dalam dan Luar Segitiga

dikumpulkan pada 29 Januari 2022

Kerjakan soal berikut dengan baik dan benar

1. Perhatikan gambar berikut ini.
   
   
   
   
   
   Jika panjang AB = 8 cm, BC = 9 cm, dan AC $= \sqrt{145}$ cm, tentukan
          a. luas  ABC;
          b. keliling  ABC;
          c. panjang jari-jari lingkaran dalam segitiga ABC.
   
   Jawab:
   
   a. Karena $\bigtriangleup ABC$ merupakan segitiga siku-siku maka berlaku
   
   
   Luas $\displaystyle \bigtriangleup ABC= \frac{1}{2}\times BC \times AB = \frac{1}{2}\times 9 \times 8 = 36$ cm$^2$
   
   b, Keliling $\bigtriangleup ABC = AB + BC + AC = 8 + 9 + \sqrt{145}=17 + \sqrt{145}$
   
   
   c. panjang jari-jari lingkaran dalam $\bigtriangleup$ 
   
   
   $\displaystyle r = \frac{\begin {matrix}luas & \bigtriangleup ABC \end {matrix}}{s}=\frac{36}{\frac{1}{2}\times \begin {matrix}keliling & \bigtriangleup ABC\end {matrix}}=\frac{36}{\frac {1}{2}\times(17+\sqrt{145})}=\frac{72}{17+\sqrt {145}}$ 
   
   
   
2. Perhatikan gambar berikut ini!
   
   
   
   
   
   diketahui panjang AB = BC = AC = 9 cm. Tentukan 
           a. luas ' ABC;
           b. panjang jari-jari lingkaran luar ' ABC. 
   
   Jawab
   
   a. $\displaystyle s =\frac{1}{2}\times (AB+BC+AC) =\frac {1}{2}\times 3 \times 9 = \frac{27}{2}$ cm
   
           luas $\displaystyle \bigtriangleup ABC =\sqrt{s(s-AB)(s-BC)(s-AC)}=\sqrt{ \frac{27}{2}\times  ( \frac{27}{2}-9)^3}$
   
           luas $\displaystyle \bigtriangleup ABC=\sqrt{ \frac{27}{2}\times  \left ( \frac{9}{2} \right )^3}=\frac{27}{2}=\frac{81}{4}\sqrt 3$ cm$^2$
   
   
   
   b. Panjang jari-jari lingkaran luar $\bigtriangleup ABC$
   
   
   $\displaystyle r =\frac{AB\times BC\times AC}{4\times \begin {matrix} luas & \bigtriangleup ABC \end {matrix}}=\frac{3\times 9}{\frac {81}{4} \sqrt 3}=\frac{4}{3\sqrt 3}=\frac{4\sqrt 3}{9}$ cm
   
   
   
   
3. Panjang sisi miring suatu segitiga siku-siku adalah 26 cm dan panjang salah satu sisi siku-sikunya 10 cm. Tentukan
           a. panjang jari-jari lingkaran dalam segitiga;
           b. panjang jari-jari lingkaran luar segitiga.
   
   Jawab
   
   
   a = 10, c = 26 dan  b = ? .Gunakan phytagoras untuk mencari b
   
   
   $b=\sqrt {c^2-a^2}=\sqrt{26^2-10^2}=\sqrt{676-100}=\sqrt{576}=24$
   
   
   Luas segitiga $\displaystyle =\frac{1}{2}\times a \times b = \frac{1}{2} \times 10 \times 24 = 120$ cm$^2$
   
   
   $\displaystyle s = \frac{1}{2}(a + b + c)=\frac{1}{2}(10+24+26)=30$   
   
   a. $\displaystyle r =\frac {luas \bigtriangleup}{s}=\frac{120}{30}=4$ cm
   
   b. $\displaystyle r =\frac{a\times b \times c}{4\times luas \bigtriangleup}=\frac{10\times 24\times 26}{4 \times 120}=13$ cm
   
   
   
4. Panjang sisi-sisi sebuah segitiga adalah 26 cm, 28 cm, dan 38 cm. Hitunglah
           a. panjang jari-jari lingkaran dalam segitiga;
           b. panjang jari-jari lingkaran luar segitiga.
   
   Jawab:
   
   
   $a=26, b=28$ dan $c=38$
   $\displaystyle s=\frac{1}{2}(a+b+c)=\frac{1}{2}(26+28+38)=46$
   
   
   luas $\bigtriangleup =\sqrt {s(s-a)(s-b)(s-c)}=\sqrt{46(46-26)(46-28)(46-38)}=\sqrt{46\times 20\times 18 \times 8}=24\sqrt {230} $ cm$^2$
   
   a. panjang jari-jari lingkaran dalam segitiga =
   
   
   $\displaystyle r =\frac {luas \bigtriangleup}{s}=\frac{24 \sqrt{230}}{46}=\frac{12 \sqrt 230}{23}$ cm
   
   b. Panjang jari-jari lingkaran luar segitiga =
   
   
   $\displaystyle r =\frac {a \times b \times c}{4\times luas \bigtriangleup}=\frac{26\times 28 \times 38}{4 \times 24 \sqrt{230}}=\frac{1729 \sqrt 230}{1380}$ cm
   
   
   
5. Panjang sisi-sisi sebuah segitiga adalah 8 cm, 15 cm, dan 17 cm. Hitunglah
           a. panjang jari-jari lingkaran dalam segitiga;
           b. panjang jari-jari lingkaran luar segitiga
   
   jawab:
   
   Jawab:
   
   
   $a= 8, b=15$ dan $c=17$
   
   
   $\displaystyle s=\frac{1}{2}(a+b+c)=\frac{1}{2}(8+15+17)=20$
   
   
   luas $\bigtriangleup =\sqrt {s(s-a)(s-b)(s-c)}=\sqrt{20(20-8)(20-15)(20-17)}=\sqrt{20\times 12\times 5 \times 3}=60 $ cm$^2$
   
   
   
   a. Panjang jari-jari lingkaran dalam segitiga =
   
   
   $\displaystyle r =\frac {luas \bigtriangleup}{s}=\frac{60}{20}=3$ cm
   
   b. Panjang jari-jari lingkaran luar segitiga =
   
   
   $\displaystyle r =\frac {a \times b \times c}{4\times luas \bigtriangleup}=\frac{8\times 15 \times 17}{4 \times 60}=8,5$ cm

==== Selamat Mengerjakan ====

catatan:
Sebagai bahan acuan untuk mengerjakan soal tersebut, dapat kalian baca pada tautan berjudul "Menentukan panjang jari-jari lingkaran dalam dan luar segitiga"

Jari-jari lingkaran dalam dan luar segitiga.

Menentukan Panjang Jari - Jari Lingkaran Dalam dan Luar Segitiga

Setelah kita membahas materi tentang sabuk pada lingkaran, kali ini kita akan mempelajari materi mengenai bagaimana menentukan panjang jari-jari lingkaran dimana tiga titik pada lingkaran tersebut masing-masing menyinggung sisi-sisi pada segitiga. Pada pembahasan kali ini. kita akan mengenal istilah jari-jari lingkaran dalam segitiga dan jari-jari lingkaran luar segitiga. Namun sebelum kita mengenal lebih jauh mengenai hal itu, kita akan diperkenalkan terlebih dahulu teknik menghitung luas segitiga bila diketahui panjang ketiga sisinya.

A. Menentukan Luas Segitiga Bila Diketahui Panjang Sisi-Sisinya.

 Perhatikan gambar berikut ini:

Gambar di atas menunjukan bahwa segitiga $\bigtriangleup ABC$ memiliki panjang sisi AB = c, AC = b dan BC = a. Jika kita menarik garis tegak lurus BC dan melalui A, maka akan didapatkan titik potong garis tegak lurus tersebut dengan garis BC. Misalkan saja titik potong tersebut adalah D. Apabila kita andaikan panjang BD = x, maka panjang CD = a - x. Dengan demikian berdasarkan rumus Phtagoras kita dapatkan:

$t^2 = c^2 - x ^2$   dan  $t^2 = b^2 - (a-x)^2$ ........ persamaan 1

jika kita subtitusikan kedua persaman tersebut maka kita akan mendapatkan   

                $c^2 - x ^2 = b^2 - (a-x)^2$ 

                $c^2 - x ^2 = b^2 - a^2+2ax- x^2$

                $c^2 - b ^2 + a^2= 2ax$

                $\displaystyle x = \frac {c^2 - b ^2 + a^2}{2a}$

kita subtitusikan persamaan terakhir ke dalam bagian pertama persamaan 1 didapat

                 $t^2 = c^2 - x ^2$

                 $\displaystyle t^2 = c^2 - \left ( \frac{c^2-b^2+a^2}{2a} \right) ^2$    ingat      $p^2 - q^2 = (p-q) (p+q)$     

                 $\displaystyle t^2 = \left ( c+\frac{c^2-b^2+a^2}{2a} \right) \left ( c-\frac{c^2-b^2+a^2}{2a}  \right )$

                 $\displaystyle t^2 = \left (\frac{2ac+c^2-b^2+a^2}{2a} \right) \left ( \frac{2ac-(c^2-b^2+a^2)}{2a}  \right )$

                 $\displaystyle t^2 = \left (\frac{c^2-b^2+a^2+2ac}{2a} \right) \left ( \frac{-c^2+b^2-a^2+2ac}{2a}  \right )$

                 $\displaystyle t^2 = \left (\frac{c^2+2ac+a^2-b^2}{2a} \right) \left ( \frac{b^2-(c^2-2ac+a^2)}{2a}  \right )$

                 $\displaystyle t^2 = \left (\frac{(c+a)^2-b^2}{2a} \right) \left ( \frac{b^2-(c-a)^2}{2a}  \right )$

                 $\displaystyle t^2 = \left (\frac{(c+a+b)(c+a-b)}{2a} \right) \left ( \frac{(b+c-a)(b-(c-a))}{2a}  \right )$ 

                 $\displaystyle t^2 = \left (\frac{(c+a+b)(c+a-b)}{2a} \right) \left ( \frac{(b+c-a)(b-c+a))}{2a}  \right )$  ..... persamaan 2

Sekarang misalkan $\displaystyle s =\frac {1}{2}\times keliling$ $\displaystyle \bigtriangleup ABC=\frac{1}{2}(a+b+c)$, maka

                 $a+b+c =2s$       $c+a = 2s - b$      $a+b = 2s - c$       $b+c=2s -a$   ..... persamaan 3

Sehingga dari persamaan 2 dan persamaan 3 diperoleh

                $\displaystyle t^2 = \left (\frac{(c+a+b)(c+a-b)}{2a} \right) \left ( \frac{(b+c-a)(b-c+a))}{2a}  \right )$  

               $\displaystyle t^2 = \left (\frac{(s)((2s-b)-b)}{2a} \right) \left ( \frac{((2s-a)-a)((2s-c)-c)}{2a}  \right )$  

               $\displaystyle t^2 = \left (\frac{(2s)(2s-2b)}{2a} \right) \left ( \frac{(2s-2a)(2s-2c)}{2a}  \right )$  

              $\displaystyle t^2 = \left (\frac{2(2s)(s-b)}{2a} \right) \left ( \frac{2(s-a) 2(s-c)}{2a}  \right )$  

              $\displaystyle t^2 = \left (\frac{4(s)(s-b)(s-b)(s-a)}{a^2} \right) $  

              $\displaystyle t = \frac{2}{a}\sqrt{(s)(s-b)(s-b)(s-a) } $  

Karena Luas $\bigtriangleup ABC = \frac {1}{2}\times a \times t$, maka dari persamaan terakhir diperoleh

               Luas $\displaystyle \bigtriangleup ABC = \frac {1}{2}\times a \times \frac{2}{a}\sqrt{(s)(s-b)(s-b)(s-a) }$

               Luas $\bigtriangleup ABC = \sqrt{(s)(s-b)(s-b)(s-a) }$

            

Dengan demikian kita sudah dapat menyimpulkan bahwa

Rumus :
" Jika sebuah segitiga memiliki panjang sisi masing-masing adalah a, b dan c, maka luas segitiga tersebut adalah 

               Luas $=\sqrt {s (s-a)(s-b)(s-c)}$        dimana $\displaystyle s = \frac{1}{2}\times (a+b+c)$

B. Jari-jari Lingkaran  Dalam Segitiga

Sekarang perhatikan gambar berikut ini

Pada gambar di atas nampak a, b, dan c adalah panjang sisi masing-masing segitiga. Setiap sisi segitiga tersebut bersinggungan dengan sebuah lingkaran yang terdapat pada segitiga tersebut. Kita akan menunjukan hubungan antara luas segitiga, panjang sisi segitiga dan jari-jari lingkaran dalam segitiga tersebut.

Perhatikan bahwa segitiga $\bigtriangleup ABC$ terbagi dalam 3 buah segitiga yakni : $\bigtriangleup AOB. \bigtriangleup AOC$  dan  $\bigtriangleup BOC$. Jari-jari lingkaran yang terdapat di dalam $\bigtriangleup ABC$  merupakan tinggi dari setiap segitiga tersebut. Dengan demikian 

Luas $\bigtriangleup ABC =$ luas $\bigtriangleup AOB$ + luas $\bigtriangleup AOC$ + luas $\bigtriangleup BOC$

                   Luas $\displaystyle \bigtriangleup ABC =\frac {1}{2}. c . r + \frac {1}{2}.b.r + \frac{1}{2}.a.r$

                   Luas $\displaystyle \bigtriangleup ABC =\frac {1}{2} r . (a+b + c)$

karena (a+b+c) = 2s dan luas segitiga  $=\sqrt {s(s-a)(s-b)(s-c)}$  maka kita dapatkan 

                   Luas $\displaystyle \bigtriangleup ABC =\frac {1}{2} r . (a+b + c)$

                   Luas $\displaystyle \bigtriangleup ABC =\frac {1}{2} r . 2s$


                   $\displaystyle r= \frac {\begin {matrix} luas&\bigtriangleup ABC \end {matrix}}{s}=\frac{\sqrt {s(s-a)(s-b)(s-c)}}{s}$

Dengan demikian kita dapat menyimpulkan bahwa

"Panjang jari-jari lingkaran dalam segitiga sama dengan luas segitiga dibagi setengah dari keliling segitiga, yakni:

  $\displaystyle r= \frac {\begin {matrix} luas&\bigtriangleup ABC \end {matrix}}{s}=\frac{\sqrt {s(s-a)(s-b)(s-c)}}{s}$

C. Jari-jari Lingkaran Luar Segitiga

Untuk memahami jari-jari lingkaran luar segitiga, kalian bisa mengamti gambar berikut ini:

Gambar di atas menunjukan bahwa sebuah segitiga $\bigtriangleup ABC$ berada di dalam lingkaran yang berjari-jari. Setiap sudut dari $\bigtriangleup ABC$ menyinggung lingkaran yang berpusat di O. Panjang sisi $AB =c , BC = a$ dan $AC = b$. Kita akan menentukan apakah ada hubungan antara jari-jari lingkaran dengan panjang ketiga sisi segitiga tersebut. Sebagai gambaran awalny, coba kalian membuat garis AD yang tegak lurus dengan garis BC. Kemudian kalian buat perpanjangan garis AO sampai memotong lingkaran di titik E. Maka kalian akan mendapati gambar seperti berikut ini:

 

Kalau kalian amati, AE merupakan diameter lingkaran dan $\angle ACE$ merupakan sudut keliling yang menghadap busur $\overset{\frown}{AE}$.  Berdasarkan sifat sudut keliling dan sudut pusat,  maka kita dapatkan:

$\angle ACE =\frac {1}{2} \times \angle AOE =\frac {1}{2}\times 180^o=90^o$

kemudian perhatikan $\angle ABC$ dan $\angle AEC$. Kedua sudut tersebut menghadap busur yang sama yakni $\overset{\frown}{AC}$. Maka berdasarkan sifat semua sudut keliling yang menghadap busur yang sama, kita dapatkan

$\angle ABC = \angle AEC$

Dengan demikian kita dapat menyimpulkan bahwa $\bigtriangleup ABD$ sebanding dengan $\bigtriangleup AEC$ sehingga berlaku hubungan perbandingan yakni:

$\displaystyle \frac{AE}{AB}=\frac {AC}{AD}$

$\displaystyle \frac{2r}{c}=\frac {b}{AD}$      $\Leftrightarrow$   sebab AE adalah diameter lingkaran

$\displaystyle AD=\frac {b\times c}{2r}$  ............... persamaan (i)

Sekarang kita amati kembali $\bigtriangleup ABC$. Dengan mensubtitusikan persamaan (i) maka kita dapatkan luas segitiga tersebut adalah

Luas $\displaystyle \bigtriangleup ABC = \frac{1}{2} \times BC \times AD=\frac{1}{2}\times a \times \left ( \frac{b \times c}{2r} \right ) = \frac{a\times b \times c}{4r}$

atau

$\displaystyle r = \frac {a \times b \times c}{4 \times \begin {matrix} luas & \bigtriangleup ABC \end {matrix}}= \frac {a \times b \times c}{4 \sqrt{s(s-a)(s-b)(s-c)}}$

untuk  $\displaystyle s=\frac{1}{2} \times (a+b+c)$

Dengan demikian kita dapat menyimpulkan bahwa
"Panjang jari-jari lingkaran luar segitiga sama dengan hasil perkalian sisi-sisi segitiga dibagi dengan 4 kali luas segitiga tersebut, yakni :

$\displaystyle r = \frac {a \times b \times c}{4 \times \begin {matrix} luas & \bigtriangleup ABC \end {matrix}}= \frac {a \times b \times c}{4 \sqrt{s(s-a)(s-b)(s-c)}}$

untuk  $\displaystyle s=\frac{1}{2} \times (a+b+c)$

===== Selamat Belajar =====