Contoh soal Hots tentang Persamaan garis singgung persekutuan lingkaran

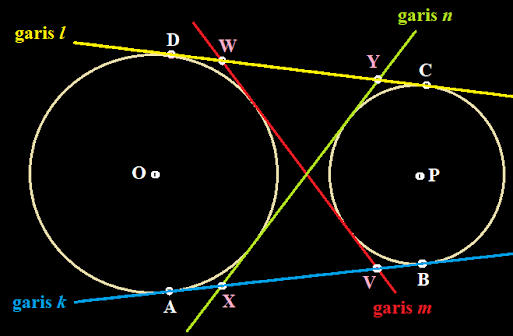
1. Lingkaran I dan lingkaran II masing-masing titik pusatnya terletak di titik O dan titik P. Kedua lingkaran tersebut berada dalam kedudukan terpisah satu dengan yang lainnya.  Garis k dan garis l adalah garis singgung persekutuan luar kedua lingkaran tersebut. Garis k menyinggung lingkaran I di titik A dan menyinggung lingkaran II di titik B. Garis l menyinggung lingkaran I di titik D dan menyinggung lingkaran II di titik C. Selain itu garis m dan garis n adalah garis singgung persekutuan dalam kedua lingkaran tersebut. Garis m memotong garis k dan garis l masing-masing di titik V dan di titik W. Garis n memotong garis k dan l di titik X dan di titik Y.
   
   Tunjukan bahwa AB = CD = VW = XY
   
   
   

   
   
   
   
   jawab:         
   
   perhatikan gambar berikut ini:|
   
   
   
   
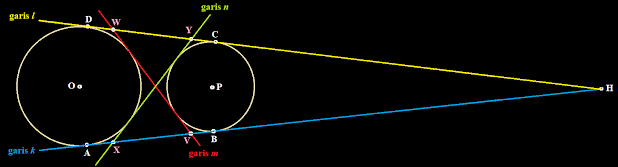
   Jika kita membuat perpanjangan garis k dan garis l sedemikian sehingga berpotongan pada titik H, maka akan kita dapatkan
                                                         AB = AH - BH
                                                         CD = DH - CH
   
   Tetapi berdasarkan sifat garis singgung lingkaran yang berpotongan di luar lingkaran didapat
                                                         AH = DH
                                                         BH = CH
   Akibatnya
                                                      AB = AH - BH
                                                      AB = DH - CH = CD ..... persamaan 1
   
   Kemudian, misalkan titik Q, R, S, dan T masing-masing merupakan titik singgung garis persekutuan dalam lingkaran dan U adalah titik potong garis singgung persekutuan dalam tersebut seperti pada gambar berikut ini:
   
   
   

   
   

   
   
   Nampak pada gambar  bahwa 
                CD = CY + YD
                QY = YS +  QS
   
   Tetapi berdasarkan sifat dua garis singgung yang berpotongan di luar lingkaran kita tahu bahwa :
                CY  = YS
                YD = QY
   
   Oleh karena itu 
                 CD = CY + YD = YS + QY = YS + (YS + SQ) = 2 YS + QS ...... persamaan 2
   
   Selain itu pada gambar nampak:
                 AB = AX + XB
                 XS = XQ + QS
   
   berdasarkan sifat dua garis singgung yang berpotongan di luar lingkaran kita tahu bahwa :
                 XS = XB
                 AX = XQ
   
   Oleh karena itu didapat :
                AB = AX + XB = XQ + XS = XQ + (XQ + QS) = 2 XQ + QS ,,,,,,,, persamaan 3
   
   Karena AB = CD maka dari persamaan 2 dan persamaan 3 diperoleh
               AB = CD
   2 YS + QS = 2 XQ + QS
          YS      =        XQ   ........ persamaan 4
   
   dari persamaan 1, persamaan 2 dan persamaan 4 
   
                       AB = CD = YD + CY = QY + YS = YQ + XQ = XY
   
   Dengan demikian telah ditunjukan bahwa AB = CD = XY.
   
   Sekarang, dengan analogi yang sama kita juga dapat menunjukan bahwa AB = CD = VW, yakni 
   
   Nampak pada gambar  bahwa 
                CD = WD + CW
                RW = WT +  TR
   Tetapi berdasarkan sifat dua garis singgung yang berpotongan di luar lingkaran kita tahu bahwa :
                WD  = WT
                RW  = CW
   
   Oleh karena itu 
                 CD = WD + CW = WT + RW = WT + (WT + TR) = 2 WT + TR ...... persamaan 5
   
   Selain itu pada gambar nampak:
                 AB = AV + VB
                 VT = VR + TR
   
   berdasarkan sifat dua garis singgung yang berpotongan di luar lingkaran kita tahu bahwa :
                 VT = AV
                 VB = VR
   
   Oleh karena itu didapat :
                AB = AV + VB = VT + VR = (VR +TR)+ VR = 2 VR + TR ,,,,,,,, persamaan 6
   
   Karena AB = CD maka dari persamaan 5 dan persamaan 6 diperoleh
               AB = CD
   2 VR + TR = 2 WT + TR
          VR      =        WT   ........ persamaan 7
   
   dari persamaan 1, persamaan 5 dan persamaan 7 
   
                       AB = CD = WD + CY = WT + RW = VR + RW = VW
   
   Dengan demikian telah ditunjukan bahwa AB = CD = VW
   
   Karena AB = CD = XY dan AB = CD = VW maka berlaku AB = CD = VW = XY
   

==== Good Luck ====

Teorema Steiner pada Garis singgung lingkaran

Teorema Steiner

Pada pembahasan kali lalu, kita telah mempelajari teorema Pitot mengenai hubungan lingkaran dengan bidang segi empat yang sisi-sisinya merupakan garis singgung lingkaran tersebut. Pada kali ini kita akan membahas mengenai teorema lain yang berkaitan dengan hubungan tersebut, yakni teorema Steiner. Perbedaan antara teorema Steiner dengan teorema Pitot terletak pada kedudukan lingkaran tersebut terhadap bidang segiempatnya. Pada teorema Pitot, lingkaran berada di dalam bidang segiempat. Sebaliknya pada teorema Steiner, lingkaran berada di luar bidang segiempat tersebut. 

• Teorema 1

Jika terdapat segiempat ABCD dimana setiap sisinya merupakan garis yang bersinggungan dengan sebuah lingkaran di luar segiempat tersebut maka berlaku rumus AB - CD = AD - BC 

 

Bukti:

Kasus 1

Misalkan titik P, Q, R, dan S masing-masing adalah titik singgung garis AB, AD, BC dan DC pada lingkaran. Maka pada gambar nampak bahwa

AB = AP - BP

AD = AQ - DQ 

Jika kedua persamaan tersebut dikurangkan maka kita dapatkan

AB - AD = (AP-BP) - (AQ - DQ) ....... persamaan 1

Akan tetapi dari sifat dua buah garis singgung lingkaran yang berpotongan di luar lingkaran, nampak bahwa 

AP = AQ

BP = BR 

DS = DQ

CR = CS

Dengan mensubtitusikan keempat persamaan terakhir ke dalam persamaan 1 diperoleh

                                                     AB - AD = (AP - BP) - (AQ - DQ)

                                                     AB - AD = (AQ - BR) - (AQ - DS)

                                                     AB - AD =       DS       -       BR

                                                     AB - AD = (DC + CS) - (BC + CR)

                                                     AB - AD = (DC + CS) - (BC + CS)

                                                     AB - AD =        DC      -        BC 

                                           AB - DC =        AD      -        BC 

 

Dengan demikian terbukti 

Kasus 2

Misalkan titik P, Q, R dan S masing-masing merupakan titik singgung garis AB, AD, CD dan CB seperti gambar berikut:

Pada gambar nampak bahwa :

AB = AP - BP

AD = AQ - DQ 

Jika kedua persamaan tersebut dikurangkan maka kita dapatkan

AB - AD = (AP-BP) - (AQ - DQ) ....... persamaan 2

Akan tetapi dari sifat dua buah garis singgung lingkaran yang berpotongan di luar lingkaran, nampak bahwa 

AP = AQ

BP = BS 

DR = DQ

CR = CS

Dengan mensubtitusikan keempat persamaan terakhir ke dalam persamaan 2 diperoleh

                                                  AB - AD = (AP - BP) - (AQ - DQ)

                                                  AB - AD = (AQ - BS) - (AQ - DR)

                                                  AB - AD =       DR      -       BS

                                                  AB - AD = (CD - CR) - (BC - CS)

                                                  AB - AD = (CD - CS) - (BC - CS)

                                                  AB - AD =       CD      -       BC 

                                                  AB - CD =       AD      -       BC

Dengan demikian terbukti

• Teorema 2

Jika titik A, B, C, D dan E masing-masing merupakan itik potong 4 garis singgung lingkaran di luar lingkaran tersebut seperti nampak pada gambar di bawah ini, maka AB - CD= BC - AD

 

Bukti

Misalkan titik P, Q, R dan S masing-masing merupakan titik singgung garis AB, AD, CD dan CB seperti gambar berikut:

Pada gambar nampak bahwa :

AB = BP - AP

CD = DR - CR 

Jika kedua persamaan tersebut dikurangkan maka kita dapatkan

AB - CD = (BP - AP) - (DR - CR) ....... persamaan 3

Akan tetapi dari sifat dua buah garis singgung lingkaran yang berpotongan di luar lingkaran, nampak bahwa 

AP = AQ

BP = BS 

DR = DQ

CS = CR

SE = EQ

Dengan mensubtitusikan keempat persamaan terakhir ke dalam persamaan 2 diperoleh

                                                  AB - CD = (BP - AP) - (DR - CR)

                                                  AB - CD = (BS - AQ) - (DQ - CS)

                                                  AB - CD = ((BC - CS) - (AD - DQ)) - (DQ - CS)

                                                  AB - CD = (BC - CS - AD + DQ) - (DQ - CS)

                                                  AB - CD = BC - AD 

==== Selamat Belajar ====

Teorema Pitot pada garis singgung lingkaran

Teorema Pitot pada Garis Singgung Lingkaran

Pada pembahasan sebelumnya, kalian terlah mempelajari kharakteristik dari garis singgung lingkaran beserta beberapa teorema yang mengikutinya. Pada pembahasan kali ini, kita juga akan diperkenalkan dengan beberapa teorema lain yang berhubungan dengan garis singgung pada lingkaran. Salah satu teorema yang cukup terkenal adalah teorema Pitot, Dalam ulasannya Pitot mengaitkan hubungan diantara panjang ruas segiempat yang setiap garis pada sisi segiempat bersinggungan dengan lingkaran yang terdapat di dalam segiempat tersebut. 

A. Segitiga Sama Kaki dan Garis Singgung Lingkaran

Jika $\bigtriangleup ABC$ adalah segitiga di dalam lingkaran dan garis m adalah garis singgung lingkaran di titik A, maka $\bigtriangleup ABC$ merupakan segitiga sama kaki jika garis m sejajar dengan garis BC.

hubungan garis singgung lingkaran dan
segitiga sama kaki di dalam lingkaran

 B. Teorema Pitot

• Teorema 2

Jika setiap sisi segitiga ABC menyinggung lingkaran yang berada di dalam segitiga tersebut dan titik P adalah titik singgung pada sisi AC, maka berlaku rumus AC + PB = BC + AP

Bukti:

Misalkan titik Q dan R masing-masing merupakan titik singgung sisi AC dan BC pada lingkaran seperti pada gambar berikut:

Maka berdasarkan sifat dua garis singgung lingkaran yang berpotongan di luar lingkaran diperoleh:

QC = RC

AQ = AP

PB = BR

Jika ketiga persamaan tersebut dijumlahkan maka diperoleh 

AQ + QC + BP = BR + RC + AP

AC + PB = BC + AP 

Dengan demikian terbukti teorema tersebut

 

• Teotema 2

Jika segiempat ABCD merupakan segi empat yang sisi-sisinya merupakan garis singgung sebuah lingkaran (lingkaran berada di dalam segi empat), maka berlaku rumus AB +CD = AD +BC

Pada kasus 1

Misalkan titik P, Q, R dan S masing-masing merupakan titik singgung sisi AD, CD, BC dan AB seperti pada gambar berikut: 

Maka berdasarkan sifat dua garis singgung lingkaran yang berpotongan di luar lingkaran diperoleh:

AS = AP

SB = BR

CQ = RC

QD = PD

Jika keempat persamaan tersebut dijumlahkan maka diperoleh 

AS + SB + CQ + QD = AP + PD + BR +RC

AB + CD = AD + BC 

Dengan demikian terbukti teorema tersebut

Pada kasus 2 

Maka berdasarkan sifat dua garis singgung lingkaran yang berpotongan di luar lingkaran diperoleh:

AS = AP

SB = BQ

RD =PD 

Jika ketiga persamaan terakhir dijumlahkan maka persamaan tersebut dijumlahkan maka diperoleh:

AS + SB + PD = AP + BQ + RD ...... persamaan (*)

Akan tetapi kita tahu  bahwa

CQ = RC  

BQ = BC + CQ

RD = RC + CD

Dengan mensubtitusikan tiga persamaan terakhir ke dalam  persamaan (*) , diperoleh :

AS + SB + RD = AP + BQ + PD

AB + RC + CD = AP + BC + CQ + PD

AB + CQ + CD = AD + BC + CQ

AB + CD = AD + BC

Dengan demikian terbukti teorema tersebut

==== Selamat Belajar ====

Garis singgung persekutuan dua lingkaran

Kedudukan Garis Singgung pada Dua Lingkaran

    Pada pembahasan kali lalu, kita telah mempelajari materi tentang garis singgung dan kharakteristiknya. Pada pembahasan kali ini, kita akan mempelajari lebih lanjut mengenai garis singgung persekutuan dua lingkaran. Di dalam pembahasan ini, kita diperkenalkan terlebih dahulu perihal bagaimana kedudukan lingkaran terhadap lingkaran lain lalu kemudian dibahas mengenai kedudukan garis singgung terhadap dua lingkaran. Pada bagian terakhir kalian akan diajak untuk mengenal apa itu garis singgung persekutuan dalam lingkaran dan garis singgung persekutuan luar lingkaran dan bagaimana cara menentukan panjang garisnya. Untuk mempersingkat waktu, baiklah kita awali terlebih dahulu dengan topik pembahasan kita mengenai kedudukan dua lingkaran.

A. Kedudukan Dua Lingkaran

Jika terdapat dua lingkaran masing-masing lingkaran L1 berpusat di P dengan jari-jari R dan lingkaran L2 berpusat di Q dengan jari-jari r di mana R > r maka terdapat beberapa kedudukan lingkaran sebagai berikut

1. L2 terletak di dalam L1 dengan P dan Q berimpit, sehingga panjang PQ = 0. (gambar 1)
   Dalam hal ini dikatakan L2 terletak di dalam L1 dan konsentris (setitik pusat). 
   
   
2. L2 terletak di dalam L1 dan PQ < r < R. (gambar 2)
   Dalam hal ini dikatakan L2 terletak di dalam L1 dan tidak konsentris. 
   
   
3. L2 terletak di dalam L1 dan PQ = r = 1 2 R, sehingga L1 dan L2 bersinggungan di dalam. (gambar 3)
   
   
4. L1 berpotongan dengan L2 dan r < PQ < R. (gambar 4)
   
   
5. L1 berpotongan dengan L2 dan r < PQ < R + r. (gambar 5)
   
   
6. L1 terletak di luar L2 dan PQ = R + r, sehingga L1 dan L2 bersinggungan di luar. (gambar 6) 
   
   

L1 terletak di luar L2 dan PQ > R + r, sehingga L1 dan L2 saling terpisah . (gambar 7)

B. Kedudukan Garis Singgung terhadap Dua Lingkaran

        Setelah kita mengetahui bagaimana kedudukan dua lingkaran, maka pada pembahasan selanjutnya kita akan diperlihatkan bagaimana kedudukan garis singgung terhadap dua lingkaran. Hubungan garis  singgung dengan lingkaran dapat memiliki hubungan sebagai berikut:

1. Pada Gambar (i) kedua lingkaran tidak mempunyai garis singgung persekutuan.
   
   
2. Pada Gambar (ii) kedua lingkaran mempunyai satu garis singgung persekutuan. 
   
   
3. Pada Gambar (iii) kedua lingkaran mempunyai dua garis singgung persekutuan.
   
   
4. Pada Gambar (iv) kedua lingkaran mempunyai tiga garis singgung persekutuan. 
   
   
5. Pada Gambar (v) kedua lingkaran mempunyai empat garis singgung persekutuan.

Ada sebuah pertanyaan menarik bagi kalian: Jika kita mengetahui bahwa sebuah garis menyinggung kedua lingkaran di dua titik, apakah kita dapat menentukan jarak kedua titik singgung tersebut? Jawaban dari pertanyaan ini akan kalian dapat ketika kita mempelajari tentang garis singgung perseketuan lingkaran, yakni garis yang menghubungkan titik singgung pada masing-masing lingkaran.. Di dalam pembahasan selanjutnya, kalian akan mengenal dua istilah penting yakni garis singgung persekutuan dalam lingkaran dan garis singgung persekutuan luar lingkaran dan mempelajari  bagaimana menentukan panjang garis singgung persekutuan dalam lingkaran dan garis singgung persekutuan luar tersebut. 

C. Garis Singgung Persekutuan Dalam Lingkaran 

        Untuk  menentukan panjang garis singgung persekutuan dalam lingkaran, kita dapat menggunakan hukum phytagoras. Perhatikan gambar berikut ini

Pada gambar di atas, garis m menyinggung dua buah lingkaran yang berpusat di titik O dan P. Titik A dan C merupakan titik persinggungan garis m  terhadap kedua lingkaran tersebut. garis OB merupakan perpanjangan garis OA dan garis BP sejajar dengan garis m. Titik D merupakan titik potong antara garis yang menghubungkan titik pusat kedua lingkaran tersebut dengan garis m. Sementara OA dan PC adalah jari-jari masing-masing lingkaran dan AC adalah panjang garis singgung persekutuan dalam lingkaran. Karena ABPC adalah persegi panjang maka kita dapatkan AB = PC dan BP = AC. 

Perhatikan, bahwa $\bigtriangleup OAD$ merupakan segitiga siku-siku dan $\bigtriangleup OBP$ sebangun dengan $\bigtriangleup OAD$. Garis OB tegak lurus dengan garis BP. Dengan menggunakan hukum Phytagoras kita dapatkan

                $OP ^2 = OB^2+BP^2 =(OA+AB)^2+AC^2= (OA+PC)^2+AC^2$

         $\Leftrightarrow$   $AC^2 = OP^2 -(OA+PC)^2$

jika kita misalkan panjang garis singgung persekutuan dalam $AC= d$, Jari-jari masing-masing lingkaran adalah OA = R  dan PC = r  serta jarak kedua lingkaran $OP =p$ maka kita dapatkan : "panjang garis singgung persekutuan dalam lingkaran adalah akar kuadrat dari kuadrat jarak kedua lingkaran dikurangi kuadrat jumlah kedua jari-jari lingkaran, yakni

$d =\sqrt{ p^2 -(R+r)^2}$

D. Garis Singgung Persekutuan Luar Lingkaran

        Untuk  menentukan panjang garis singgung persekutuan luar lingkaran, kita dapat menggunakan hukum Phytagoras. Perhatikan gambar berikut ini

Pada gambar di atas, garis m adalah garis singgung persekutuan luar kedua lingkaran di titik B dan C. Kedua lingkaran berpusat di O dan P. Garis AP sejajar dengan garis m. Ruas garis OP adalah jarak kedua titik pusat masing-masing lingkaran dan OB serta PC adalah jari-jari masing-masing lingkaran. Karena segiempat ABCP adalah persegi panjang, maka AP = BC dan AB = CP sehingga OA = OB - AB. 

Perhatikan bahwa $\bigtriangleup OAP$ merupakan segitiga siku-siku. Garis OA tegak lurus dengan garis AP. Dengan demikian kita dapat menggunakan hukum Phytagoraas yakni:

                  $OP^2 = OA^2+ AP^2=(OB-AB)^2+AP^2$

       $\Leftrightarrow$       $AP^2=OP^2-(OB-OA)^2$

Jika panjang garis singgung persekutuan luar $AP = d$, jarak kedua titik pusat lingkaran $OP = p$ dan masing-masing jari-jari lingkaran $OB =R$ dan $CP=AB=r$, maka kita dapat menyimpulkan bahwa: "Jarak garis singgung persekutuan luar kedua lingkaran sama dengan akar kuadrat dari kuadrat jarak titik pusat kedua lingkaran  dikurang kuadrat selisih kedua jari-jari lingkaran", yakni:

$ d=\sqrt{p^2-(R-r)^2}$

=== Selamat Belajar ===